 |
| Vanishing dimensions. Technical sketch. Source: arXiv:1406.2696 [gr-qc] |
Some years ago, we discussed the “Evolving Dimensions”, a new concept in the area of physics beyond the standard model. The idea, put forward by Anchordoqui et al in 2010, is to make the dimensionality of space-time scale-dependent so that at high energies (small distances) there is only one spatial dimension and at small energies (large distances) the dimension is four, or possibly even higher. In between – in the energy regime that we deal with in everyday life and most of our experiments too – one finds the normal three spatial dimensions.
The hope is that these evolving dimensions address the problem of quantizing gravity, since gravity in lower dimensions is easier to handle, and possibly the cosmological constant problem, since it is a long-distance modification that becomes relevant at low energies.One of the motivations for the evolving dimensions is the finding that the spectral dimension decreases at high energies in various approaches to quantum gravity. Note however that the evolving dimensions deal with the actual space-time dimension, not the spectral dimension. This immediately brings up a problem that I talked about to Dejan Stojkovic, one of the authors of the original proposal, several times, the issue of Lorentz-invariance. The transition between different numbers of dimensions is conjectured to happen at certain energies: how is that statement made Lorentz-invariant?
The first time I heard about the evolving dimensions was in a talk by Greg Landsberg at our 2010 conference on Experimental Search for Quantum Gravity. I was impressed by this talk, impressed because he was discussing predictions of a model that didn’t exist. Instead of a model for the spacetime of the evolving dimensions, he had an image of yarn. The yarn, you see, is one-dimensional , but you can knit it to two-dimensional sheets, which you can then form to a three-dimensional ball, so in some sense the dimension of the yarn can evolve depending on how closely you look. It’s a nice image. It is also obviously not Lorentz-invariant. I was impressed by this talk because I’d never have the courage to give a talk based on a yarn image.
It was the early days of this model, a nice idea indeed, and I was curious to see how they would construct their space-time and how it would fare with Lorentz-invariance.
Well, they never constructed a space-time model. Greg seems not to have continued working on this, but Dejan is still on the topic. A recent paper with Niayesh Afshordi from Perimeter Institute still has the yarn in it. The evolving dimensions are now called vanishing dimensions, not sure why. Dejan also wrote a review on the topic, which appeared on the arxiv last week. More yarn in that.
In one of my conversations with Dejan I mentioned that the Causal Set approach makes use of a discrete yet Lorentz-invariant sprinkling, and I was wondering out aloud if one could employ this sprinkling to obtain Lorentz-invariant yarn. I thought about this for a bit but came to the conclusion that it can’t be done.
The Causal Set sprinkling is a random distribution of points in Minkowski space. It can be explicitly constructed and shown to be Lorentz-invariant on the average. It looks like this:
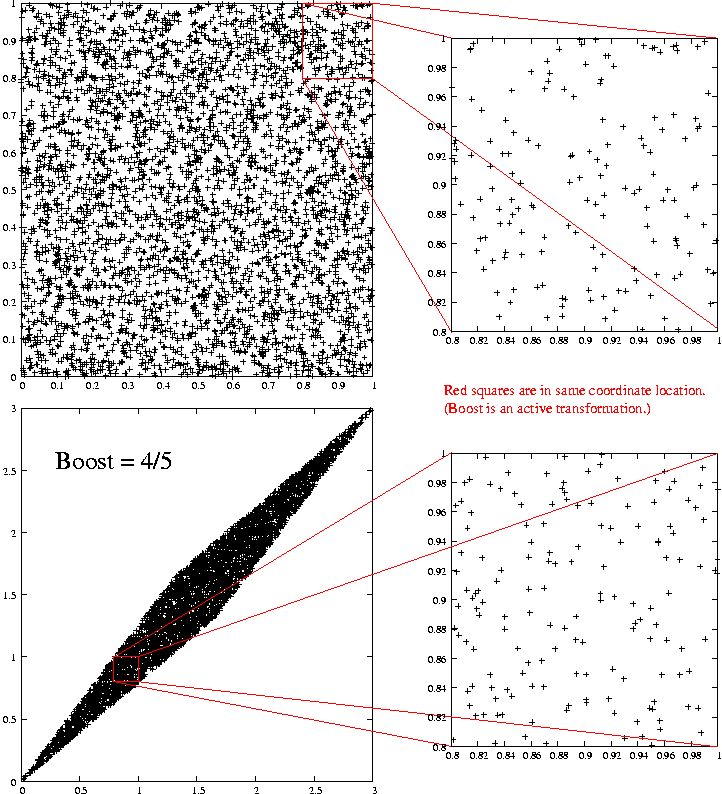 |
| Causal Set Sprinkling, Lorentz-invariant on the average. Top left: original sprinkling. Top right: zoom. Bottom left: Boost (note change in scale). Bottom right: zoom to same scale as top right. The points in the top right and bottom right images are randomly distributed in the same way. Image credits: David Rideout. [Source] |
The reason this discreteness is compatible with Lorentz-invariance is that the sprinkling makes use only of four-volumes and of points, both of which are Lorentz-invariant, as opposed to Lorentz-covariant. The former doesn’t change under boosts, the latter changes in a well-defined way. Causal Sets, as the name says, are sets. They are collections of points. They are not, I emphasize, graphs – the points are not connected. The set has an order relation (the causal order), but a priori there are no links between the points. You can construct paths on the sets, they are called “chains”, but these paths make use of an additional initial condition (eg an initial momentum) to find a nearest neighbor.
The reason that looking for the nearest neighbor doesn’t make much physical sense is that the distance to all points on the lightcone is zero. The nearest neighbor to any point is almost certainly (in the mathematical sense) infinitely far away and on the lightcone. You can use these neighbors to make the sprinkling into a graph. But now you have infinitely many links that are infinitely long and the whole thing becomes space-filling. That is Lorentz-invariant of course. It is also in no sensible meaning still one-dimensional on small scales. [Aside: I suspect that the space you get in this way is not locally identical to R^4, though I can’t quite put my finger on it, it doesn’t seem dense enough if that makes any sense? Physically this doesn’t make any difference though.]
So it pains me somewhat that the recent paper of Dejan and Niayesh tries to use the Causal Set sprinkling to save Lorentz-invariance:
“One may also interpret these instantaneous string intersections as a causal set sprinkling of space-time [...] suggesting a potential connection between causal set and string theory approaches to quantum gravity.”
This interpretation is almost certainly wrong. In fact, in the argument that their string-based picture is Lorentz-invariant they write:
“Therefore, on scales much bigger than the inverse density of the string network, but much smaller than the size of the system, we expect the Lorentz-invariant (3+1)-dimensional action to emerge.”Just that Lorentz-invariance which emerges at a certain system size is not Lorentz-invariant.
I must appear quite grumpy going about and picking on what is admittedly an interesting and very creative idea. I am annoyed because in my recent papers on space-time defects, I spent a considerable amount of time trying to figure out how to use the Causal Set sprinkling for something (the defects) that is not a point. The only way to make this work is to use additional information for a covariant (but not invariant) reference frame, as one does with the chains.
Needless to say, in none of the papers on the topic of evolving, vanishing, dimensions one finds an actual construction of the conjectured Lorentz-invariant random lattice. In the review, the explanation reads as follows: “One of the ways to evade strong Lorentz invariance violations is to have a random lattice (as in Fig 5), where Lorentz-invariance violations would be stochastic and would average to zero...” Here is Fig 5:
 |
| Fig 5 from arXiv:1406.2696 [gr-qc] |
Unfortunately, the lattice in this proof by sketch is obviously not Lorentz-invariant – the spaces are all about the same size, which is a preferred size.
The recent paper of Dejan Stojkovic and Niayesh Afshordi attempts to construct a model for the space-time by giving the dimensions a temperature-dependend mass, so that, as temperatures drop, additional dimensions open up. This begs the question though, temperature of what? Such an approach might make sense maybe in the early universe, or when there is some plasma around, but a mean field approximation clearly does not make sense for the scattering of two asymptotically free states, which is one of the cases that the authors quote as a prediction. A highly energetic collision is supposed to take place in only two spatial dimensions, leading to a planar alignment.
Now, don’t get me wrong, I think that it is possible to make this scenario Lorentz-invariant, but not by appealing to a non-existent Lorentz-invariant random lattice. Instead, it should be possible to embed this idea into an effective field theory approach, some extension of asymptotically safe gravity, in which the relevant scale that is being tested then depends on the type of interaction. I do not know though in which sense these dimensions then still could be interpreted as space-time dimensions.
In any case, my summary of the recent papers is that, unsurprisingly, the issue with Lorentz-invariance has not been solved. I think the literature would really benefit from a proper no-go theorem proving what I have argued above, that there exist no random lattices that are Lorentz-invariant on the average. Or otherwise, show me a concrete example.
Bottomline: A set is not a graph. I claim that random graphs that are Lorentz-invariant on the average, and are not space-filling, don’t exist in (infinitely extended) Minkowski space. I challenge you to prove me wrong.

Euclid arises from postulates. Cartography falsifies Euclid. Euclid's Fifth Postulate was rewritten. Physics arises from postulates. Newton fell to Maxwell. GR and QM cannot overlap, SUSY is not empirical, dark matter and axion detectors are sterile . Physics must be...parameterized. One sine wave cycle is not an odd polynomial, though they are arbitrarily indistinguishable, except past end points.
ReplyDeletePhysical theory empirically fails given illusions of knowledge. Grant-funding demands searches under streetlights. This rewards theoretic processes but not orthogonal experimental discovery. Vacuum is observed to be chiral anisotropic toward hadronic matter. Macroscopically test for it in at least five different ways. Streetlights are not needed after sunrise.
Sabine,
ReplyDeleteI find this blog topic most interesting.
I do not think it is possible to refute your thoughts on it, but so far I find little to disagree with your view of things. Of course I do not have the benefits of training formally yet in my own studies which I have posted informally recently I do have a consistent view on a different or more general level. So if there are errors, obvious ones, I have accidentally made the same errors.
I downloaded the arVix paper and find it rather primitive and frankly do not see anything original. Perhaps it is so in the sense that no one has asserted this dimensional phase changing and reversal of the roles of dimensions and energy as physical observable's before - an appeal to novelty I suppose. That and the growing experimental evidence of paradoxes and anomalies closer to our understanding by our better instruments at hand.
We can in fact cite precursors to some of the general but vague earlier ideas.
I think we need to look closer at the relation to singularities in general which with the right intuition and interpretations do what this paper claims to explain - or more likely is closer among many such alternatives that could do so just as well. But when things are synthetic they border on philosophic issues which could be the case but harder to prove. - I am telling you nothing we do not already know- or as the author said is already present as evidence around us (that epiphany is new, apparently).
Relating it to the cosmic background is a sort of colorful journalism that perhaps in its own way the author advances science interest- as well as with some papers that seem so contradictory, perhaps wrong it excites a response, justified or not, just like Motl's recent defense of his quantum ideas declaring a general complexity idea as unoriginal. I do not see how that could advance string theory, I do see how if space is so absolutely random that the averaging of such entities may relate to physical space. QM gravity in a sense could be like a flat jellyfish that takes in maximum water then jets it out into a smaller opening to jet, but in what direction in free three space? Or if in the micro-world our mouths are very wide to take in the plankton recovering energy.
Feynman said after all there was room at the bottom. We can send space probes very far if small, what if infinitely small?
Uncle Al,
ReplyDeleteChirality is most important but is not the primary foundation of things, we have to dig deeper.
I liked your idea in normal 3D where we talk about ellipsoids of an axes and it forms a unity (say volume) but I have a game called butter with the dimensions of the unit volume one times the golden ratio and its inverse. If we subdivide it by all combinations of k t 1 cubed there is a small volume left over of the same proportions and so on.
In three space, perhaps where we are limited to standard or dogmatic models, the drunk around a lampost in his random walk does not necessarily come back to his starting place.
I noticed a tweet here that finds quasi crystals in nature, I thought these were already observed...in layers for example. But the internal arrangement in a Penrose tile in 2 or 3 space can be independent in orientation that the tiling it is in. So to the butter can be totally independent in its abstract transformations like Rubik's cubes in its sub-regions.
The finite cannot be distinguishable as to what is the inside or outside, say a collection of points. If these are cubes, say the 7 internal ones as we unfold a hypercube, we note that if there is intrinsic motion four describe something time like and four around it in a torus something space like. or conversely.
And also, everyone:
http://arxiv.org/pdf/0801.3306v4.pdf
This paper seemed to me something to suggest haunting similarity to my own long used system. We really need to define dimension and information better.
Does not complexity vanish also in our models if in this sense they do with dimensions? Harder to read the fingerprints of patterns directly formed from smaller gene elements?
In general directed motion or chiral spin is time centered and Naturally euclidean while a linear motion is directed thru or is quantized into the adjacent dimension as in production of pairs. coivariance and invariance can be seen in the same model and linear spectral fractal like order as space filling can be arbitrary, even unobservable. Nature preserves Lorentz.
But I use Quasized rather than Qlassical or Quantized.
Consider Lorentz invariance leaking non-symmetric affine connection (Christoffel connection. "Spin density" quadratic terms appear in the Lagrangian. Invariance leakage is 1.2×10^(-10) m/s^2 Milgrom acceleration. Eötvös experiments are 5×10^(-14) difference/average sensitive. Tight package, arXiv:1310.4009, 1209.3086. Enantiomorphic space group alpha-quartz single crystal test masses are maximum chiral-divergence mass distributions. Falsifying experiments must offend physics. Anything postulate-allowed cannot find postulate violation.
ReplyDelete58 words including a quantitative experiment versus 363 words without testable consequences.
I liked the Technical Sketch immensely.
ReplyDeleteUncle Al,
ReplyDeleteI am not sure I have made the points clear. You have made very good intuitive points. How did Euclid know to call it the parallel postulate and not a theorem way back for example?
To talk of leaky ideas in space as gravity (that may correspond to some sort of reduction of chirality to hadron structure) seems to me a vague artifact thought or experiment needs to explore.
Five ways? 105 parameters? how is it you suggest that, with certainty? It is hard to force a five dimensional shadow into a three space structure that fills crystal spaces in the first place.
I agree with Sabine that the hyperbolic extensions may only go so far and presently seem to explain things locally. But there are exotic ideas that we vaguely imagine go beyond this. And it can be seen as a matter of "points " or nodes simply connected or not. It cannot be rigidly set into separate even or odd formulas. But both descriptions may apply from some viewpoint. These alph null points may be classes. I mean the dots thought stars are now considered clusters of stars and so on.
So we have say 4 natural dimensions or 10 Newtonian as the same description. The four planes in the drawing in the article we should think of as Branes for example of possible supersymmetry where it belongs (as it vanishes in the standard theory)
Each brane can be thought of as multidimensional and a Feynman diagram.
But there can be an ordered, or spectral sequence of adjacent branes, a time or superdetermined time so to speak that addresses the arrow of time or entropy. One direction would reverse every other brane. Thus cyclic universes are not ruled out nor inflation models by these thoughts as to what can be observed in the cosmic background.
That said, that we can have an idea of total uncertainty applies also as a grounding for the foundations as well. That is to say that induction averaging is a valid way to do science also where we find what is physical.
In space structure we can have three viable forms of a coherent organism... but if we apply this to natural four space there can be a chaotic system of independent forms which could not self correct to an organism so in biology this is no surprise in thoughts on code.
Given say the triads in music of 24 chords, major, minor, diminished and augmented it naturally splits into two systems of twelve chords wherein three of one type compliments one of another type across the keys. This is the chirality of a cosmological principle as Crick asked concerning evolving anything in terms of local coherent replication.
Artificial intelligence is that what we think of as transhuman is also transmechanism.
Our distinction between exponential and linear growth is not as clear as we try to arrange.
I love the super-synchronicity effect I find on the internet (starting with a poem a week site where poems between poets on the same theme were answered at the same posting.)
ReplyDeleteI checked on Hogg's research just now. Someone I follow who is an astronomer from a random blogspot when I set up my blog. His thoughts and methods I am sure you all will find interesting.
I found he has an article that relates to my view of the topic at hand:
http://hoggresearch.blogspot.com/2014/06/quadratures-and-cosmological-inferences.html
He does not post much but sometimes he has a clear attempt to explain or try new methods, especially in interpreting astronomical data by statistical methods.
ReplyDeleteDesperate times elicit desperate ideas.
Meanwhile far more natural approaches are ignored.
We must turn to the real world for observational clues.
Dear Sabine,
ReplyDeleteThank you very much for writing an entry about our recent paper. The issues that you mention are indeed important. However, they are addressed in the text.
The temperature that you are asking about is the temperature of the fields that live on the string worldsheet. By identifying the time coordinate on the worldsheet with that in the target space, this temperature becomes the same as in the target space (our big universe). It is this temperature that dictates when the dimensions will be excited (or de-excited).
About the Lorentz invariance, in section III, we start from the (1+1)d action in UV and arrive to the Lorentz invariant action in (3+1)d in IR. This construction is explicit.
About the analogy with the causal sets and sprinkling, at the fundamental level, the string is all there is in our model. So it is fundamentally a (1+1)d construct at high temperatures. When the temperature drops, new dimensions open up in the form of new directions where the string can propagate. Thus, the string starts intersecting itself. These intersections can be viewed as the lattice sites of a random lattice if the configuration is frozen, or a space-time sprinkling if the situation is dynamical (intersections keep appearing and disappearing randomly). At high temperatures these extra directions are not available and the string is simply a (1+1)d object.
I hope this helps.
Best wishes,
Dejan
Dejan:
ReplyDelete1) What's the "temperature of the universe" in a lepton-lepton collision? To even define something like a temperature you need to have background fields, some type of mean field approximation which, for scattering events is a really bad approximation. It is for that matter also a bad approximation to use the 'temperature of the universe' on, say, our planet, but then the difference doesn't matter.
2) Your 'explicit construction' is, when I understand that correctly, Lorentz-invariant in a certain energy (temperature) regime, which just means that it's not Lorentz-invariant.
3) You fail to show that the intersection points are distributed Lorentz-invariantly. I am telling you it can't be done. There is no analogy with causal sets. You claim that there is one but this is just words and images. As I said in my post: Show me a Lorentz-invariant network (string network or otherwise) in 3+1 dimensional space and I'll shut up.
Best,
B.
The dimensionality of Universe is indeed scale dependent, but in different way, than the theorists apparently expect. For example the dark energy is an example of the "evolving dimensions" at the large scale. Of course, if you include it in the equations, they become linear again. The same applies to short scale. The physicists are apparently confused as hell (the same applies to string theorists who seek for violation of inverse square law for gravity, while ignoring - actually intentionaly excluding - the Cassimir and dipole forces from measurements).
ReplyDeleteAnyway, a nice and informative post. The hard work must be appreciated.
Hi, I came here through LM's blog. I hope you don't mind :-)
ReplyDeleteWhat do you think about this paper? Are these networks Lorentz-Invariant?
http://arxiv.org/pdf/1310.6272v1.pdf
And I have also a question: to define the spectral dimension, you are using something akin to ranom walks on graphs by means of Markov processes, right? And the spectral dimension is defined by means of diffusion distance in terms of the Markov process. Are use using a classical random walk on graph or are you using quantum random walk on the graph?
http://arxiv.org/pdf/quant-ph/0303081.pdf
PS: this topic caught my attention because I am using very similar mathematics in a competely unrelated field - machine learning and neuroscience. I am using an algorithm named "diffusion map" to define diffusion distances and perform network clustering on brain networks.
Cheers, Mephisto
Yorick (Mephisto),
ReplyDeleteWell, looking at what Lubos writes, I should first clarify that a minimal length doesn't necessarily have anything to do with discreteness. There are examples where you get a minimal length without discreteness and examples where you have discreteness but no minimal length, details on this are in my review. For this reason a minimal length (defined properly) can be perfectly compatible with Lorentz-invariance, though it tends to cause other problems.
Regarding the paper that you mention. First, you don't gain anything in rewriting Minkowski space into other coordinates. Having said that, the network that they construct is that of a single observer - an observer at rest. You can do this, and you can do this Lorentz-COVARIANTLY. Ie, the network depends on the observer. As I said in my post, yes, you can do this but you need an additional reference frame (in this case the restframe of the observer). The point is if you do this for all observers and combine their networks to get the complete space-time, the result will be space-filling.
Regarding the spectral dimension - this is probably a misunderstanding: "I" am not doing anything. This is not a topic I work on myself. I wrote some while back on the spectral dimension in ASG and if I recall correctly they used a classical random walk, but you can just look up the paper... Best,
B.
Dear Sabine,
ReplyDeleteIn our Lagrangian in the section "Symmetron Dimensional Confinement" the temperature in question comes from radiation (energy density of radiation in the universe gives the mass term to the fields which are "dimensions"). You can modify the Lagrangian to include the vacuum energy density if you want. Two leptons colliding are not going to change the temperature of the environment, so they will collide in (3+1)d today (except in a variant of our model where the geometry of the lattice is such that partcles with finite energy can see the cross-over). To deactivate dimensions thermally at least in some small region you need many particles colliding so that finite temperature is established, like we have in cosmic rays collisions. It is intriguing that some cosmic ray experiments indeed show alignment of the showers.
Yes, our induced action is Lorentz invariant in IR. But as we said, a particle propagating from a distant GRB toward us (that Fermi is seeing) is propagating in a low temperature regime, so it is seeing (3+1)d, not (1+1)d.
It is true that we did not show that the intersection points are distributed in a Lorentz invariant way, but random Poison sprinkling should do this in general.
Best,
Dejan
Dejan,
ReplyDeleteFirst, I strongly doubt that the particle in cosmic ray events are thermalized in any sensible meaning. For all I know they aren't even properly thermalized in heavy ion collisions at RHIC, or at least that's a matter of controversy.
Second, you don't only talk about cosmic ray events but also about LHC collisions. Wasn't that planar alignment one of your predictions?
Third, the statement that a particle that propagates has a low energy isn't Lorentz-invariant in itself. It may be low energy in the Earth restframe, but in some other restframe it can be arbitrarily high. Again, you're breaking Lorentz-invariance.
Forth, you write
"It is true that we did not show that the intersection points are distributed in a Lorentz invariant way, but random Poison sprinkling should do this in general."
I am telling you that the intersection points cannot be distributed by the random Poisson sprinkling that is used in CS (if you mean some other sprinkling, please let me know which), unless the network is spacefilling. You saying that it "should do this" is not very convincing. Try to write down your network, or draw it if you must, start with points, then try to add connections so that it remains Lorentz-invariant. You should see quickly what I mean. Best,
Sabine
Dumb question :
ReplyDeleteDoes the evolving dimension idea gives any insight on the nature of time?
/*Does the evolving dimension idea gives any insight on the nature of time*/
ReplyDeleteApparently not, as you can see - it's much easier to deduce it from understanding of the nature of space-time instead. If you would live as a waterstrider at the water surface and if you would observe it with its own ripples, then the space dimensions would fuse with temporal dimensions for you at distance.
Als,
ReplyDeleteNo, it doesn't, you assume the signature has one -1 (ie one time-dimension). Best,
B.
Dear Sabine,
ReplyDeleteI agree that cosmic ray events may not be fully thermalized, but they are much closer to high temperature regime than collisions of just two leptons.
In our paper we tried to point out that the dimensions always exist as degrees of freedom in the theory, but they are not excited at high temperatures. Once you excite them at a certain temperature, the resulting network has its own properties. It may be space-filling (especially in the quantum picture), or it may resemble a frustrated string network - classical random lattice. If it is space-filling, then Lorentz invariance is exact, but the LHC should not see anything. If it is a frozen classical network, then LHC (or some machine operating near the cross-over scale that depends on the geometry if the lattice) should see planar events, elliptic jets (but no new particles). Lorentz invariance might be broken in some way, but not obviously in a way that Fermi puts the limits on. For example one of the photons should propagate above the cross over scale and one below in order to get the difference in propagation. However, both photons from Fermi were in GeV range, so none of them probes the cross-over regime.
Also, you need the space-filling network to recover 100% of Lorentz invariance. But the process should converge fast, meaning that a network which is say 80% space-filling could recover 99.99% Lorentz invariance (I am just throwing the numbers, but from people who work on this topic I have heard that the convergence is indeed fast).
And yes, the first degree of freedom that is excited should be the time-like coordinate. So time should come to the existence first, then everything else.
Best,
Dejan
Hi Dejan,
ReplyDeleteThanks, I sense some convergence here.
So you agree that Lorentz-invariance is violated. I have no clue what you mean with "80%" Lorentz-invariant, I don't know what you are quantifying here. What you should be quantifying is the coupling of the particles to the LI violating structure of the network. It will almost certainly appear as a violation of momentum conservation and show up in the mass-shell relation (and thus in the dispersion relation). The relevant scale that will enter there is almost certainly the scale at which the 3rd spatial dimension 'closes', ie some TeV. As you know LIV at that scale is ruled out the extremely high precision, thus my conclusion is that your model is almost certainly ruled out already on the grounds of violating Lorentz-invariance.
I know I've been telling you this since at least 2010, apparently quite unsuccessfully, so I hope you forgive me for not contacting you this time before I wrote this blogpost. Without showing in exactly which way your emergent 3+1 space-time picture is Lorentz-invariance-violating and how the propagation of particles is affected by this, the vanishing dimensions remain on the level of being not even wrong. You are implicitly claiming either
a) there exist randoms graphs in 3+1 Minkowski space that are on the average Lorentz-invariant (you seem to be saying that this is not what you claim in your papers, but this seems to be what Niayesh is saying) or
b) Your model does violate Lorentz-invariance at the TeV scale, but this LIV cannot be captured in an effective field theory treatment.
Both of these are very bold claims that are almost certainly wrong. Either way, if you can show one of these statements to be correct, this would certainly be very interesting, more interesting indeed than the vanishing dimensions themselves.
Best,
Sabine
Dear Sabine,
ReplyDeleteYou are oversimplifying my statements. In the model with Niayesh, the string network can be space-filling and the space-time is continuous, especially in a quantum picture where you have to sum over all the possible configurations of the string. In this limit Lorentz invariance is exact, I think you would agree with that. In this case dimensions can be deactivated only thermally, so no experiment with a few particles can see less than 3 continuous dimensions.
I feel that somehow you are attacking the second option where the string network freezes in a form of a random lattice. I agree that this option is more problematic, but I disagree that is already excluded. You are probably thinking of Fermi and similar experiments. In that context we are pretending that we understand how quantum fields (particles) interact with the space-time structure, which we certainly do not. We treat the particles in the context of quantum theory but the space-time is still classical. And our experience tells us that very often when we think semi-classically we get confused (e.g. information loss paradox). I respect the limits coming from Fermi but I am not sure if we can take them face value. After all, if the fundamental theory is lower dimensional, then the number 10^19 GeV is just an effective low energy value. The true scale of quantum gravity (or whatever is the fundamental theory of space-time) may be much larger than that, or even infinite. In that case naïve LIV effects would be suppressed by infinite factors. I admit that this is far fetched, but we do not know the rules of the game that we are playing, and we should not pretend that we do.
Best,
Dejan
Dejan Stojkovic
ReplyDeleteMathematical operations in a sense can vanish too. Octonions and all that. So, what about 8+1 formulism?
What is the temperature of that ninth (technically not there) gluon?
I find it appealing to imagine from zero (and it is called the zeroth law isn't it?) an evolving sense of dimensions conceptually. I find it as interesting to imagine that matter evolves likewise - or whole inflation universes and so on. Was Einstein right to reject Weyl on this and his gauge theory ideas where do they apply in our science today?
Einstein remarked that in many ways four space was a simpler geometry.
Let us consider my game of Calyptic cubes, six cubes of six faces any four of them on the surface may match. There are 36 faces. These are colored by nine quilt patterns of four colors. Now as a simple exercise ignoring surface arguments of colored tangled strings but think about the ways to arrange them that the puzzle comes out over all. It is rather hard to do, requires a complex mathematical view. (later I tied it to Hessan polytopes that involves 3's.)
But my point is that once you make a set of them it is very easy for even a child to solve the color matching. The complexity was in trying to figure it out. Of course nature helps, or math does by there being exactly 9 such quilt patterns.
qsa
ReplyDeleteinteresting thoughts. I wonder how Penrose concludes twistors define gravity.
Two points and something between them, two lines and something between them... superposition by projection and so on.
I think the problem is that we cannot at the foundations distinguish points and lines as such or time or distance between them. We can model them, yes.
Quasic Principle: at singularity the ground state of universe of two objects, such as spheres or points, are neither continuous or discontinuous. There may be a between or not be a between. In a deeper sense we can imagine all apparent separated areas as continuous (absurdly we could walk from a spot on the earth to a spot on the moon for example.)
Otto,
ReplyDeleteVery good questions, but to do them justice I will answer later since it is very late our time.
But the answer is really there in all my write ups , however I know it is tedious and time consuming to go through them carefully.
Hi Dejan,
ReplyDeleteWell, if you think I am oversimplifying then I think you are trying to produce fog to hide the problems with your model
1. "In this limit Lorentz invariance is exact, I think you would agree with that. In this case dimensions can be deactivated only thermally..."
No, I don't agree with that. If Lorentz-invariance is exact then it's exact, period. You cannot 'deactivate' it at some energy scale without violoating Lorentz-invariance. Which energy scale, of what and in which frame? As I said - the only way I see that you can make sense of this is in some eft framework and then you'll probably reproduce something like ASG. In this case though I don't know whether it's still reasonably to interpret the dimensions as space-time dimensions.
2. "I feel that somehow you are attacking the second option where the string network freezes in a form of a random lattice. I agree that this option is more problematic, but I disagree that is already excluded. You are probably thinking of Fermi and similar experiments."
Fermi is not a good example since the allegedly possible Fermi modification is already long ruled out by other experiments, literally hundreds of them. Fermi was supposed to test deformations of LI, not violations, different thing altogether. I don't know why you keep even talking of that - you have no business with deformations of LI, you are actually breaking Lorentz-invariance.
Yeah, I agree that you don't know how the particles interact with the background because you don't have a model for the background. I am saying if you want the model to have any plausibility, you have to show that this interaction does not produce higher-order LIV couplings, and I cannot see how you can avoid this. The proof is on you. You're the ones making such big claims, you have to show that it's possible. I am seriously disappointed that you (and your coauthors) keep evading this issue. Best,
Sabine
qsa: Had to delete your comment. No links to personal websites, please read comment rules.
ReplyDeleteCan I just say that Lubos Motl is mistaken here. The principle of Lorentz invariance isn't some sacred cow. Nor is the principle of equivalence. See SpaceTime Mission: Clock Test of Relativity at Four Solar Radii. You should expect to measure the fine structure constant varying with gravitational potential. I say that as a "relativist" who knows that a principle does not demand absolutely exactness. Accelerating through space is not exactly the same as being in a gravitational field.
ReplyDeleteSabine,
ReplyDeleteI deleted the link.
Although my idea does no address the issue of Lorentz in-variance and dimensions directly at this point (I am sure it will eventually), but I think it gives an idea how to look at these issues.
My idea is based on random points, and upon calculation of all possible relations, the laws of physics (QM,QFT) automatically arise. I think the secret is that time is not involved directly, it becomes just a change of state, many ideas have conjectured that.
This idea implements exactly what Penrose was trying to prove with spinors. That is that particles and space-time(in my case only space) are emergent from a single entity. That single entity is exactly two random points where a pair makes a line. And so it has a very close picture to Causal Set but without explicit time involved.
Moreover, I have noticed early on that my idea seems to be similar to buffon's needle problem but with the needle being also random. After many hours of research I finally found the connection to a mainstream theory:
http://arxiv.org/pdf/quant-ph/9902079v1.pdf
http://arxiv.org/pdf/quant-ph/0608251.pdf
With connection to Wigner's theorem. These all involve tomography which is related to Radon transforms which is the branch of geometric probability that is nothing but the generalization of Buffon's needle 1777 problem. And that makes a full circle with Penrose transform which is a relative of Radon transform.
My idea produces a lot of results, but the most astonishing one is the appearance of the mass of the electron from the simulation of these purely random numbers.
http://www.fqxi.org/community/forum/topic/1877
I am now very close to converting the simulations to standard physics mathematical representation.
Thanks for your attention
Dear Sabine,
ReplyDeleteI noticed that your words are becoming progressively stronger. But I guess this is just your style, nothing personal.
Lorentz invariance is exact in the subset of dimensions which are already open. It is broken from the prospective of a full 10-dim theory, but these dimensions have not been excited yet, so you can't perform an experiment to see that. At the end of the process, when all dimensions open up, Lorentz invariance is manifest in all dimensions. Please mention one experiment which would tell you that Lorentz invariance is violated in a smooth, continuous (3+1)d subset with no preferred directions, when nothing else above that exists yet.
About the reference frame, the situation is the same as in the Big Bang. Just set our metric g_{\mu_nu} in our original Lagrangian which is induced by the excited string to be FRW. Then any observer who lives in that space sees exactly what we see today. There is no preferred frame.
About Fermi, it was actually you who mentioned that in a random lattice variant of our model the dispersion relation will be modified (that is was Fermi and similar experiments claim to limit). I was referring to that statement.
Best wishes,
Dejan
Sabine,
ReplyDeleteI'm not sure you aren't breaking one of the cardinal rules: never assume things! Also, never assume Lubos is correct. You, of all people, should know that.
Solid state physics has a lot to teach us here. As different materials cool or warm they undergo phase changes. These phase changes are sudden and discontinuous. You would be hard pressed to create something equivalent to a "thermal" Lorentz Invariance equation. It probably can't even be done. Why do you assume that this is a necessary thing to understand the underlying dynamics of changes in spacetime with thermal changes?
If we stipulate that "Lorentz-COVARIANTLY. Ie, the network depends on the observer" and there are infinitely many observers. Do we recover Lorentz-invariance over transformations from one observer's network to another?
ReplyDeleteOtto,
ReplyDeleteIn my post I said that the electron mass appears and that is really astonishing. But I do the same simulation using one time the Real number system and again using Integer numbers and the result is perplexing, the electron mass result is pale by comparison.
Both systems give approximately the same results at large distances, however, at short distances they diverge strongly starting at 346. What is amazing is that while the Reals work fairly well with a nice CFT type behavior, the Integer seems to have both amazing properties(no CFT though) plus a strange outcome where the proton size sit at first 5 units.
if electron Compton wave is 1823 then from standard physics the proton "size" is 1823/(137+2.8)=4.75 almost 5
and only with those numbers I get proton and electron g-factors to match with experiment. If I use Reals all these quantities become zero. Moreover Because gravity in this system is when lines meet, so the Reals will have an ambiguous answer. but the Integer will have a unique answer.
So in the Reals case space would be filled with infinite points( whether infinite and countable it remains to be seen as I convert to standard mathematical physics). In the Integer case space is cutoff at around .2 proton size (1/5). So in both cases you need a very precision experiment to determine which(some have been carried out).
I gave all these "boring" and most likely unclear description just so that to give you an idea what I am going to talk about. In the next post I will talk about more directly addressing you questions.
ReplyDeletesorry, this
1823/(137+2.8)=4.75
should be(multiply)
1823/(137*2.8)=4.75
Eric,
ReplyDeleteAs with the controversial ideas of Rene Thom some results can be abrupt and discontinuous. A good point. But his system of cusps and butterfly flips was essentially embedding spherical geometry into flat Euclidean geometry, Seven forms that appear so in a flat space.
What do we mean by "underlying assumptions?" Perhaps this is the way we see the surface of something (presumably thermodynamic in the sense the area of black holes are thought to be.) Nature seems to see the idea of dimensions this way as one possibility. A point as an intersection in two space as colored yarn (which has a negative value to the content thus it allows an attractive force of gravity externally assuming it has a finite logical structure.)
I tried to question Sabine's sense of physics or give Djan's model a fair consideration. This is needed for science. This gives me a deep question: Of models of physics as the most general short of a total decoherence or chaos of a quantum idea of background, in what sense can we relate our ideas of degrees of freedom to that of changes of evolving or vanishing geometrical dimensional structures?
If such points are say the 24 faces internally of a hypercube then these have a definite connection structure, even arithmetical. (qsa has some promising comments here that suggests more than the mass of an electron involved. The dimensionless constants and integers are involved. Not to say any of us are on to a total new physics as a general state of our vision.)
So if we imagine the inside of such a hypercube of 8 cubes 12 faces in a linear cycle or 12 in a toroidal cycle the outer appearance does not necessarily distinguish loops or extensions of loops (wave like perhaps).
But if there is such abstract motion what would make it violate Lorentz? If external dimensions in fact vanish what is the temperature of the center as the Higgs to fill the standard model?
Science over a wide spectrum seems to give us some logical results.
If we can imagine distinct arrangements of such a point-sphere of shifting states as distinct and of at least linear ordinal directions over the real,
clearly there is an underlying space of 6 degrees of freedom wherein we can expect clear effects say when such 24cell entities collide. Why else would statistical methods converge to those logically in theory yet the division of the model may not have local distribution that is a unique pattern of evolving?
If we have three axes the underlying space without privileged order is 16^3 = 64^2 = 2^12 = 4096 for a start which is a little larger than the stringy landscape of lost divergences.
Hi Dejan,
ReplyDeleteNo, nothing personal, I just try to express myself as clearly as possible.
"Lorentz invariance is exact in the subset of dimensions which are already open. It is broken from the prospective of a full 10-dim theory, but these dimensions have not been excited yet, so you can't perform an experiment to see that."
This is just words. The statement "It is exact... but is broken at some temperature" does not make sense - this just means it is not exact.
My point is that you don't know that these dimensions do not couple in at low energies, you just claim they don't. I am telling you that you will generically get couplings to the dimensions that 'have not opened up yet'. You could make the same argument for all models that violate Lorentz-invariance at the Planck scale. You could say, why should we see anything at 'temperatures' below the Planck scale? Well, we should see something because experiments are sensitive to extremely small violations of this symmetry, even if they are suppressed by large energy scales. And the scale that you are talking about (some TeV), isn't even a large scale. I am telling you you have to take great care to get rid of these terms and I am sure it will not be easy.
"About the reference frame, the situation is the same as in the Big Bang. Just set our metric g_{\mu_nu} in our original Lagrangian which is induced by the excited string to be FRW. Then any observer who lives in that space sees exactly what we see today. There is no preferred frame."
?? The FRW metric is a preferred frame. You seem to be saying the preferred frame is basically that of the CMB or closely aligned with this, which is what most LIV models also assume. I think you should really derive the couplings and look up the literature on the constraints.
Regarding Fermi: Well, Fermi does set a constraint on modified dispersion relations, but this bound isn't particularly strong. There are much stronger bounds on LIV. Best,
Sabine
Dear Sabine,
ReplyDeleteThanks!
The TeV scale is relevant only if you want to solve the hierarchy problem. In principle, the dimensional crossover can happen at any arbitrary scale. The central idea is that dimensions are fields, but these fields have temperature dependent mass.
You are talking about energy dependent LIV. Particle with some energy can pick up some energy dependent corrections which add up and give you some measurable effect. However, that is quite different from temperature dependent corrections. These will be much more suppressed. Again, high energy and high temperature are quite different notions. I do not know of an experiment that can limit temperature dependent LIV.
Also, one would need systematic LIV, so that small effects can add up coherently. If you have non-systematic LIV, the effects can cancel out. Limits on non-systematic LIV are much weaker.
Just to be completely honest for the record, we did not calculate the possible LIV terms coming from our Lagrangian. But I do not expect any problems there for the reasons I mentioned.
FRW is homogeneous and isotropic, so there is no preferred frame. The Big Bang happened everywhere in an infinite universe simultaneously. It did not start from one point. You get the preferred frame only when you put some marks in it, like CMB photons, so that you can orient yourself with respect to these marks. But that is not a fundamental preferred frame. The same in our model. The string is infinite. When dimensions are excited, they are excited everywhere. If the resulting induced metric is FRW, then you get the standard cosmology.
Best wishes,
Dejan
Uncle Al,
ReplyDeleteAs the debate seems to come to a close for now your first comment of concerns stand out over the fray. I suppose it is a question of how we explore this in the details. Chiral anisotropic issues certainly need to be worked out here... Ten dimensions are not quite enough to find the needed parameters of physics which we may do so casually as well well as where there seems a necessary causation. Guess our cell phone batteries can explode if too far from controlling circuits, feedback. Lithium ion polymers seem to have limited cycling times as practically the end points of Buffon's needle should they get hot... about two years. Linear accelerators may indeed solve some problems of quantization where a photon can react to space of many independent diagonals and initial special origins (hierarchies within hierarchies)yet interfere with themselves. And of course a more general view of neutral currents. :-)
Otto,
ReplyDeleteSorry I have not had enough time to elaborate but regarding your question about twistor and gravity I shall give some references, the first which is a must read.
http://users.ox.ac.uk/~tweb/00001/
http://arxiv.org/pdf/1404.4167v1.pdf
http://www.lpthe.jussieu.fr/~yuri/n42qcd/talks/Mason.pdf
Otto,
ReplyDeleteOne clarification. When Penrose tried to implement his idea he progressively complicated the system, in my case the system goes the other way to a simplified form which is just good old Radon transform.
see this reference for the connection between Radon and Buffon's needle (in the second method)
http://www.docstoc.com/docs/61540747/The-Buffon-Needle-Problem-and-Geometric-Probability
Here is what Penrose says in the first reference
" By a simple transformation of variables, these become the helicities zero and one cases of the basic contour integral formula (Penrose 1968, 1969a) giving the linear field case of the so-called "Penrose transform" of twistor theory. The Radon transform (Radon 1917, Gel'fand Graev & Vilenkin 1966) and its generalizations may also, from a different angle, be regarded as providing models for (and generalizations of) this twistor expression."
This comment has been removed by the author.
ReplyDelete"... random graphs that are Lorentz-invariant on the average, and are not space-filling, don’t exist in (infinitely extended) Minkowski space"
ReplyDeleteSeems to me this should be a statement that can be proven?
Have to admit I have a hard time visualizing this, since naively I regard a simple Euclidean random lattice as on average isotropic.
So, if you have an on average isotropic graph for one observer you'd pick up a preferred axis when observed from a different rest frame?
qsa
ReplyDeleteThank you for the links. It will take me awhile to study them but from what I see this approach is on topic (although the comments are perhaps too wide or technical here and now.) It suggests to me many are on the right track and that there is a deeper proof (as Henning asked about in a comment.) Sabine in my estimation is leading in the debate to higher directions.
But there may be experimental proof also as Tommaso Dorigo reports from the ATLAS data on the Higgs. I would say there is one particle but is expressed in two different ways, time-like or space-like and LT ultimately conserved.
I just have a simple visualization of some three space region that is the center of a few thousands of possible combinations of deeper symmetry. These are in a sense privileged as far as initial conditions.
But this only goes to real four space, beyond that we may indeed have to have a much wider vision.
Thank you for your contribution.
Henning wrote: "So, if you have an on average isotropic graph for one observer you'd pick up a preferred axis when observed from a different rest frame?" ISTM, that all we really need is to preserve the rule that there does not exist a prefered frame for all observers (modulo communications among them). Every observer could have a frame of their own per moment in time that is in that sense prefered. What I think SR and GR prohibit is a global ordering of coordinate systems.
ReplyDeleteLI maintains the bias of symmetry all twins love.
ReplyDeleteEven if twins don't know the difference between phase transition and symmetry breaking.
Bee:
There is no difference.
With or without bias.
Hush, that simply is not true... two twins are distinct. In four space the distinction is even more subtle.
ReplyDeleteFor example:
Stephen that may not be true either as to what we consider a real physical object and not just perhaps a mathematical artifact. I can imagine a system where global ordering of coordinate systems are coherent and not forbidden where the coordinates are at least 8x8 matrices.
So this is the issue of Lorentz or its violation. I think we need to understand what Bee means by defects better, I imagine it applies more subtly than I can now picture.
This is about orthogonal relations as I see it (but I am only about in the 70's I think in understanding physics) for example I should do an experiment on a new kind of lens I cannot put into optics formulas).
But thinking Euclideanly as the the default manifold Coxeter said this was a remarkable formula:
That the sum of n dimensional orthogons equals the product of n dimensional orthogons.
But feel free to convince me otherwise.
The point is that only "normal" distributions are Lorentz invariant. Any diffeomorphism of the embedding generates an equally normal distribution. This is equivalent to saying that one random signal is indistinguishable from any other. But thinking about things, we can see that what we each have as an experience of the universe is NOT a uniform distribution. We each have a "privileged frame" of our own.
ReplyDeleteThe key to Lorentz invariance, as I understand it, is that there cannot exist a single unique privileged frame for all observers.
Stephen,
ReplyDeleteThat rings true but the issue is that privileged frames need not be unique and yet, while there are differences surely we imagine we have something in common by being in the world... but this is philosophy in that the proof escapes us also.
Does this mean we are ultimately one system or the same entity or perhaps that with respect to that part of a higher physics, normal or not, there are degrees of observation and awareness of which mere random noise is said to be quantum in some measure of our ignorance?
The asymmetry and symmetry of anything can be the same concept at some foundation. If there are different universes (in conception) two interlaced sets of privileged random information may go beyond our usual concepts of space, even two super-determined sets beyond linearity may not fill the scope of such wider space.
Do we share the same concept of a given atom? and so on...
Layperson Q.
ReplyDeleteAlice
Let's pretend you have a model that is Lorentz invariant.
Which relationships from totality explains and describes your model?
Devoted Blog Follower,
B.o.b. :)
Bob
ReplyDeleteYou're such a romantic flirt and such a square all tensor as you ponder my low rent district. But that is just the flat we share while were twixt twelve and twenty.
Your arrow of time could compliment my accidents of creation as our dreams in passion vanish into some ocean beyond our touch. But who is to say who is the expert or the lay person where such logic and size may not matter? You see, it is not always 50-50 or its it?
In these matters of 4D balancing of equations like tomcat derrogatory lubos of old my wonderland playground not thinking the rabbit may die if it is late down the rabbit hole, is a mystery you keep that way for you have no symbol for your square square space where we meet as eagles weightless in the sky for my simple triangle.
Alice
Dear Otto Waalkes
ReplyDeleteIts = is (in your sample above)
There. Much better.
I leave the rest for your spell checker to ponder.
Or are you in a hurry?
Flüchtigkeitsfehler plus haste makes waste (broken porcelain)
I'm the elephant in the room (blog).
Bob Ottifant
p.s.
Apologies to the Blog Hostess.
Which is to say SR & QM is linear and Euclidean conceptually in higher issues of GR which has analogous concepts open to speculation outside of methods as science. After a century we create and name problems in this wider background of uncharacteristizeable universe. In a sense GR as well as QM seems incomplete. Of the 256 elements of Einstein's 16 matrix of things considered at rest 36 are considered.
ReplyDeleteWe usually compute from corners which keep the phase for this subtraction of 20 and forget the alternative view of holes in the sub power set continuity not overly reductionist involving 24.
Hi Dejan:
ReplyDeleteYou write
"You are talking about energy dependent LIV. Particle with some energy can pick up some energy dependent corrections which add up and give you some measurable effect. However, that is quite different from temperature dependent corrections. These will be much more suppressed. Again, high energy and high temperature are quite different notions. I do not know of an experiment that can limit temperature dependent LIV."
As I said earlier, the only way to make sense of the "temperature" that you are talking about is to either define it from to some background field or from the collision itself.
In the first case I don't know what the background field is, but in any case if you want to couple it to the CMB restframe that is exactly what breaks the Lorentz-invariance. And no, there's nothing different in that than any other approaches that couple to an aether or something.
If you extract the energy scale from some collision then the interpretation as temperature doesn't make sense, but you get an eft in which the effect depends eg on the Mandelstam variables of the collision. That means though there's no effect for a single propagating particle (compatible with LI). As I wrote in my post, that's the only way I can make sense of your proposal.
"Also, one would need systematic LIV, so that small effects can add up coherently. If you have non-systematic LIV, the effects can cancel out. Limits on non-systematic LIV are much weaker."
I don't know what you mean with systematic or not systematic. I suppose you mean random and/or uncorrelated. A random walk gives you a nonzero standard deviation though, even though the average is zero, so I don't know how you think that avoids the problem.
"Just to be completely honest for the record, we did not calculate the possible LIV terms coming from our Lagrangian. But I do not expect any problems there for the reasons I mentioned."
Well, I do expect these problems as I have tried to tell you for some years and I really think looking at these terms is what you should be doing in order to show that the model has any credibility and is not ruled out already.
"FRW is homogeneous and isotropic, so there is no preferred frame."
It is spatially homogeneous and isotropic. Of course FRW has a preferred frame because it has a preferred time slicing (that in which the time coordinate is orthogonal to the spatial part, as is the case in both the standard and the comoving coordinates). It is usually assumed to be identical to that of the CMB.
"The Big Bang happened everywhere in an infinite universe simultaneously. It did not start from one point"
The mere fact that you can say "silmutanous" means that there is a preferred slicing.
"You get the preferred frame only when you put some marks in it, like CMB photons, so that you can orient yourself with respect to these marks. But that is not a fundamental preferred frame."
Of course it's not a fundamental frame, it comes in because there is in fact matter in our universe, but as I said earlier you need matter (or some fields or something that carries energy) to define a temperature. A temperature doesn't make sense without a preferred frame.
"The same in our model. The string is infinite. When dimensions are excited, they are excited everywhere."
If "everywhere" means "spatially everywhere" (as in your example with the Big Bang) then you do have a preferred slicing. If it means everywhere in space-time, then you have no temperature-dependence. Either way, it's not what you claim your model does.
Best,
B.
Dear Sabine,
ReplyDeleteThe temperature in our model is defined by the background fields. Fundamentally, the string is all there is. There are fields that live on the string worldsheet (we call them \phi in the text). Since we identify the time coordinate on the worldsheet and in the target space, the temperature will be the same on the worldsheet and in the target space (effectively built by the wolldsheet).
You say "A temperature doesn't make sense without a preferred frame." You have the same "problem" in the standard cosmology. What is Planck scale for one observer is not for another since energy is not Lorentz invariant.
Systematic vs. non-systematic LIV issue is described in a nice review here http://relativity.livingreviews.org/Articles/lrr2005-5/fulltext.html
Non-systematic LIV are much more difficult to constrain.
Finally, Horava gravity violates LI explicitly and blatantly, so would you say its is useless to study it?
Probably I should not have ended with a question, because we will never end this debate online. I respect your points of view, and will be very happy to discus them with you once we meet again. It is always very useful to talk to someone like you, just for the reality check.
Bets wishes,
Dejan
Hi Dejan,
ReplyDelete"You have the same "problem" in the standard cosmology. What is Planck scale for one observer is not for another since energy is not Lorentz invariant."
No, it's not the same problem because you know how the metric couples to matter fields, but nobody knows how your network couples to matter, effectively, in the low energy limit.
I never said that LIV is ruled out in all forms and under all circumstances. I said that it is strongly constrained, how strong the constraints are depends on the coupling. This is why I am saying you should look at the coupling. As long as you don't check this your model just doesn't reproduce the standard model to the present precision.
Best,
B.