First Day of Fall 2007

The first day of fall this year will be on September 23, 2007. More precisely, the autumnal equinox will be at 9:51 UT that day, which means that the Sun will be crossing the celestial equator from north to south at that moment sharp. Thus, on September 23, the Sun will rise exactly in the East, and set exactly in the West, for all places in the world. Moreover, the time span between sunrise and sunset will be 12 hours, and equal the time span between sunset and sunrise - this equality of day and night is at the origin of the Latin name "equinox", which means equal night [1].

When I was a kid, I could understand fairly well how the seasons come about because the Earth's axis is tilted by roughly 23° with respect to the plane in which it is orbiting the Sun, called the ecliptic by the grown-ups. Playing around with a torch and an apple is good to get a feeling what is going on, and what happens when the days and nights are roughly equal. So, I could make sense of September 23 as the first day of fall - however, I remember I was extremely skeptical when my mum told me that the beginning of fall that year was at, say, 12:21 sharp. What a nonsense, I thought, how on Earth can on know this date so precisely, to the minute? Today, I know that there is an easy answer, but that, in fact, this answer just hides the question I had asked myself more than 25 years ago.

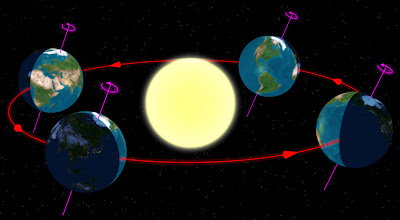Relative orientation of the Earth and the Sun at the first days of spring, summer, fall, and winter, respectively, The first day of fall corresponds to the position of Earth in the foreground. (Source: Wikipedia on the Equinox)

The easy answer as to the exact moment of the equinox goes as follows: If we want to introduce a coordinate system on the celestial sphere, in order to denote the positions of stars and planets, we can use longitude and latitude as we do on a globe: The North Pole is the point around which the night sky seems to rotate - close to Polaris - and the equator, where, for example, the stars of Orion are located, is the great circle corresponding to the equator on Earth. On the sky, these coordinates are called right ascension (corresponding to longitude) and declination (corresponding to latitude).

Now, because of the tilt of the Earth's axis, the declination of the Sun changes during the year (the right ascension changes also, giving rise to all kinds of astrological complications, but that doesn't play a role here). In the summer of the Northern hemisphere, it has a declination of up to +23.5°, which means that it rises high in the sky, and doesn't even set below the horizon at polar latitudes. In the Northern winter, declination will be negative, down to -23.5°, meaning short days and low culminations at noon. Thus, between summer and winter, the declination of the Sun has to change smoothly from about +23.5° to about -23.5°. Of course, there should be one precise moment when the declination is exactly 0.00° - that's the equinox. This year, this will happen at 9:51 UT - more precisely even, at 09:51:08 UT, according to the data of the US Naval Observatory.

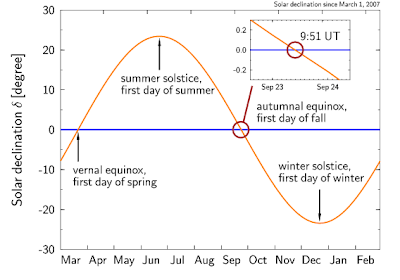The declination of the Sun since March 1, 2007. At the solstices, the declination takes extreme values: the Sun reaches its highest, respectively lowest, position in the sky. At the equinoxes, the declination is exactly zero. The curve looks similar to a sine curve, but it is more complicated function. (Data from the US Naval Observatory)

Of course, this easy answer isn't a real answer at all. There are two obvious questions left open: How can one, first of all, define a coordinate system in the sky that is that precise that it makes sense to define the exact moment when the Sun will cross the celestial equator? And then, how precisely can the actual position of the Sun be known? These are, in fact, difficult questions, and to answers them was one of the main tasks of the big National Observatories, such as Greenwich, or the US Naval Observatory.

Defining coordinates in the sky is a subtle task, because of the problems to identify some really fixed points. The right ascension for example is measured along the celestial equator starting at the vernal equinox. However, the tilt of the Earth's axis is not fixed in space - due to the torque of the Sun and the Moon, the Earth is precessing, and for this reason, the point of the vernal equinox wanders around the celestial equator once every 26,000 years. There are other problems with the motion of the Earth's axis. Even the ecliptic is not completely fixed with respect to far-away stars, because not all planets are exactly within one plane, thus causing so-called secular variations of the inclinations of the orbits. And then, as astronomers in the 19th century had to notice, even the "fixed stars" are not fixed: Some of them have proper motions so large that they cannot easily be used as references to define a coordinate system.

Defining celestial reference frames today is achieved by sources much further away than stars: Quasars are radio sources in cosmological distances, and thy do not move in the sky. Fortunately, combining radio telescopes by Very Large Baseline Interferometry allows an extremely precise determination of the position of quasars, which is used to fix a coordinate system. The orbits of the planets, and the coordinates of the Sun, can be calculated and measured very precisely with respect to this coordinate system.

What leaves me with one question I am scratching my head about: How does one measure to a high precision the position of the Sun on the celestial sphere? After all, it is not a neat small pointlike source, but has quite a large extension. From a quick search at the ADS database, I have learned that in the 1970s, this was still done in the traditional way, using a zenith tube at Herstmonceux, then the location of the Greenwich observatory in England. It may be that also in the measurement of the position of the Sun, VLBI methods have taken over: For example, precise timing of the occulations of quasars by the Sun may provide very reliable solar coordinates. So, there are still enough puzzeling questions to think about on long autumn evenings. Perhaps someone of our readers knows?

There is one good news, at least for those of us living in the Northern hemisphere: Because the Earth is closer to the Sun in winter, with the perihelion reached around January 3, fall and winter are shorter than spring and summer. And in 179 days, we will be again at the vernal equinox, and spring will begin.

---

[1] Restrictions apply: The Sun will rise exactly in the east on those places on Earth where sunrise is at 9:51 UT, i.e. along a line somewhere on the Atlantic Ocean. Moreover, due to the extension of the Sun's disk and the effect of atmospheric refraction, the Sun is visible already when in fact it is, geometrically speaking, still below the horizon. This means that actually, the day is a little bit longer on September 23 than the night.

[2] Plenty of data can be obtained from the Data Services of the Astronomical Applications Department of the U.S. Naval Observatory. For example, from the table of Earth's Seasons Equinoxes, Solstices, Perihelion, and Aphelion, here is an excerpt covering the next few years:

                  d  h                      d  h  m           d  h  m
2007                      2007
Perihelion  Jan   3 20    Equinoxes  Mar   21 00 07    Sept  23 09 51
Aphelion    July  7 00    Solstices  June  21 18 06    Dec   22 06 08

2008                      2008
Perihelion  Jan   3 00    Equinoxes  Mar   20 05 48    Sept  22 15 44
Aphelion    July  4 08    Solstices  June  20 23 59    Dec   21 12 04

2009                      2009
Perihelion  Jan   4 15    Equinoxes  Mar   20 11 44    Sept  22 21 18
Aphelion    July  4 02    Solstices  June  21 05 45    Dec   21 17 47

2010                      2010
Perihelion  Jan   3 00    Equinoxes  Mar   20 17 32    Sept  23 03 09
Aphelion    July  6 11    Solstices  June  21 11 28    Dec   21 23 38

2011                      2011
Perihelion  Jan   3 19    Equinoxes  Mar   20 23 21    Sept  23 09 04
Aphelion    July  4 15    Solstices  June  21 17 16    Dec   22 05 30

Moroever, there is a very nice feature to plot maps and views of Earth that show day and night across the globe.

---

TAGS: astronomy, first day of fall, equinox