|
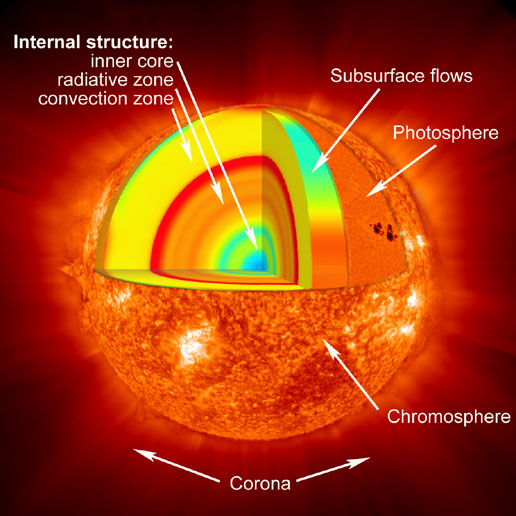
| Conference Photo: Experimental Search for Quantum Gravity 2012. |
The third installment of our conference "Experimental Search for Quantum Gravity" just completed. It was good to see both familiar faces and new ones, sharing a common interest and excitement about this research direction. This time around the event was much more relaxing for me because most of the organizational work was done, masterfully, by Astrid Eichhorn, and the administrative support at Perimeter Institute worked flawlessly. In contrast to 2007 and 2010, this time I also gave a talk myself, albeit a short one, about the paper we discussed here.
All the talks were recorded and can be found on PIRSA. (The conference-collection tag isn't working properly yet, I hope this will be fixed soon. You'll have to go to "advanced search" and search for the dates Oct 22-26 to find the talks.) So if you have a week of time to spare don't hesitate to blow your monthly download limit ;o) In the unlikely event that you don't have that time, let me just tell you what I found most interesting.
For me, the most interesting aspect of this meeting was the recurring question about the universality of effective field theory. Deformed special relativity, you see, has returned in the reincarnation "relative locality" as to boldly abandon locality altogether after the problem could no longer be ignored. It still doesn't have, however, a limit to an effective field theory. A cynic might say "how convenient," considering that 5th order operators in Lorentz-invariance violating extensions of the standard model are so tightly constrained you might as well call them ruled out.
If you're not quite as cynic however, you might take into account the possibility that the effective field theory limit indeed just does not work. That, it was pointed out repeatedly -- among others by David Mattingly, Stefano Liberati and Giovanni Amelino-Camelia -- would actually be more interesting than evidence for some higher order corrections. If we find data that cannot be accommodated within the effective field theory framework, such as for example evidence for delayed photons without evidence for 5th order Lorentz-invariance violating operators, that would give us quite something to think about.
I agree: Clearly one shouldn't stop looking just because one believes to know nothing can be found. I have to add however that the mere absence of an effective field theory limit doesn't convince me there is none. I want to know why such a limit can't be made before I believe in this explanation. For all I know it might be absent just because nobody has made an effort to derive it. After all there isn't much of an incentive to do so. As the German saying goes: Don't saw on the branch you sit on. That having been said, I understand that it would be exciting, but I'm too skeptic myself to share the excitement.
A related development is the tightening of constraints on an energy-dependence of the speed of light. Robert Nemiroff gave a talk about his and his collaborator's recent analysis of the photon propagation time from distant gamma ray bursts (GRB). We discussed this paper here. (After some back and forth it finally got published in PRL.) The bound isn't the strongest in terms of significance, but makes it to 3σ. The relevance of this paper is the proposal of a new method to analyse the GRB data, one that, given enough statistics, will allow for tighter constraints. And, most importantly, it delivers constraints on scenarios in which the speed of highly energetic photons might be slower as well as on the case in which it might be faster than the photons with lower energy. And for an example on how that is supposed to happen, see Laurent Freidel's talk.
A particularly neat talk was delivered by Tobias Fritz who summarized a simple proof that a periodic lattice cannot reproduce isotropy for large velocities, and that without making use of an embedding space. Though his argument works so far for classical particles only, I find it interesting because with some additional work it might become useful to quantify just how well a discretized approach reproduces isotropy or, ideally, Lorentz-invariance, in the long-distance limit.
Another recurring theme at the conference was dimensional reduction at short distances which has recently become quite popular. While there are meanwhile several indications (most notably from Causal Dynamical Triangulation and Asymptotically Safe Gravity) that at short distances space-time might have less than three spatial dimensions, the ties to phenomenology are so far weak. It will be interesting to see though how this develops in the coming years, as clearly the desire to make contact to experiment is present. Dejan Stojkovic spoke on the model of "Evolving Dimensions" that he and his collaborators have worked on and that we previously discussed here. There has however, for all I can tell, not been progress on the fundamental description of space-time necessary to realize these evolving dimensions.
Noteworthy is also that Stephon Alexander, Joao Magueijo and Lee Smolin have for a while now been poking around on the possibility that gravity might be chiral, ie that there is an asymmetry between left- and right-handed gravitons, which might make itself noticeable in the polarization of the cosmic microwave background. I find it difficult to tell how plausible this possibility is, though Stephon, Lee and Joao all delivered their arguments very well. The relevant papers I think are this and this.
I very much enjoyed James Overduin's talk on tests of the equivalence principle, as I agree that this is one of the cases in which pushing the frontiers of parameter space might harbor surprises. He has a very readable paper on the arxiv about this here. And Xavier Calmet is among the brave who haven't given up hope on seeing black holes at the LHC, arguing that the quantum properties of these objects might not be captured by thermal decay at all. I agree with him of course (I pointed this out already in this post 6 years ago), yet I can't say that this lets me expect the LHC will see anything of that sort. More details about Xavier's quantum black holes are in his talk or in this paper.
As I had mentioned previously, the format of the conference this year differed from the previous ones in that we had more discussion sessions. In practice, these discussion sessions turned into marathon sessions with many very brief talks. Part of the reason for this is that we would have preferred the meeting to last 5 days rather than 4 days, but that wasn't doable with the budget we had available. So, in the end, we had the talks of 5 days squeezed into 4 days. There's a merit to short and intense meetings, but I'll admit that I prefer less busy schedules.