“As the universe expands and dark energy remains constant (negative pressure) then where does the ever increasing amount of dark energy come from? Is this genuinely creating something from nothing (bit of lay man’s hype here), do conservation laws not apply? Puzzled over this for ages now.”
-- pete best
“When speaking of the Einstein equation, is it the case that the contribution of dark matter is always included in the stress energy tensor (source term) and that dark energy is included in the cosmological constant term? If so, is this the main reason to distinguish between these two forms of ‘darkness’? I ask because I don’t normally read about dark energy being ‘composed of particles’ in the way dark matter is discussed phenomenologically.”
-- CGT
Dear Pete, CGT:
Ahead, allow me to clarify that your questions refer to “dark energy” but are specifically about the cosmological constant which is a certain type of dark energy. For all we know, the cosmological constant fits all existing observations. Dark energy could be more complicated than that, but let’s start with the cosmological constant.
Einstein’s field equations can be derived from very few assumptions. First, there’s the equivalence principle, which can be formulated mathematically as the requirement that the equations be tensor-equations. Second, the equations should describe the curvature of space-time. Third, the source of gravity is the stress-energy tensor and it’s locally conserved.
If you write down the simplest equations which fulfill these criteria you get Einstein’s field equations with two free constants. One constant can be fixed by deriving the Newtonian limit and it turns out to be Newton’s constant, G. The other constant is the cosmological constant, usually denoted Λ. You can make the equations more complicated by adding higher order terms, but at low energies these two constants are the only relevant ones.
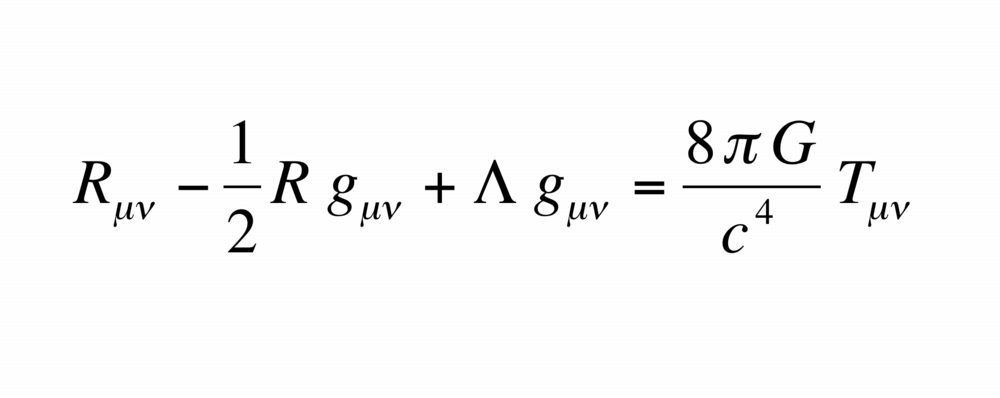 |
| Einstein's field equations. [Image Source] |
Things get difficult if one tries to find an interpretation of the rather unambiguous mathematics. You can for example take the term with the cosmological constant and not think of it as geometrical, but instead move it to the other side of the equation and think of it as some stuff that causes curvature. If you do that, you might be tempted to read the entries of the cosmological constant term as if it was a kind of fluid. It would then correspond to a fluid with constant density and with constant, negative pressure. That’s something one can write down. But does this interpretation make any sense? I don’t know. There isn’t any known fluid with such behavior.
Since the cosmological constant is also present if matter sources are absent, it can be interpreted as the energy-density and pressure of the vacuum. Indeed, one can calculate such a term in quantum field theory, just that the result is infamously 120 orders of magnitude too large. But that’s a different story and shall be told another time. The cosmological constant term is therefore often referred to as the “vacuum energy,” but that’s sloppy. It’s an energy-density, not an energy, and that’s an important difference.
How can it possibly be that an energy density remains constant as the universe expands, you ask. Doesn’t this mean you need to create more energy from somewhere? No, you don’t need to create anything. This is a confusion which comes about because you interpret the density which has been assigned to the cosmological constant like a density of matter, but that’s not what it is. If it was some kind of stuff we know, then, yes, you would expect the density to dilute as space expands. But the cosmological constant is a property of space-time itself. As space expands, there’s more space, and that space still has the same vacuum energy density – it’s constant!
The cosmological constant term is indeed conserved in general relativity, and it’s conserved separately from that of the other energy and matter sources. It’s just that conservation of stress-energy in general relativity works differently than you might be used to from flat space.
According to Noether’s theorem there’s a conserved quantity for every (continuous) symmetry. A flat space-time is the same at every place and at every moment of time. We say it has a translational invariance in space and time. These are symmetries, and they come with conserved quantities: Translational invariance of space conserves momentum, translational invariance in time conserves energy.
In a curved space-time generically neither symmetry is fulfilled, hence neither energy nor momentum are conserved. So, if you take the vacuum energy density and you integrate it over some volume to get an energy, then the total energy grows with the volume indeed. It’s just not conserved. How strange! But that makes perfect sense: It’s not conserved because space expands and hence we have no invariance in time. Consequently, there’s no conserved quantity for invariance in time.
But General Relativity has a more complicated type of symmetry to which Noether’s theorem can be applied. This gives rise to a local conservation of stress-momentum when coupled to gravity (the stress-momentum tensor is covariantly conserved).
The conservation law for the density of a pressureless fluid, for example, works as you expect it to work: As space expands, the density goes down with the volume. For radiation – which has pressure – the energy density falls faster than that of matter because wavelengths also redshift. And if you put the cosmological constant term with its negative pressure into the conservation law, both energy and pressure remain the same. It’s all consistent: They are conserved if they are constant.
Dark energy now is a generalization of the cosmological constant, in which one invents some fields which give rise to a similar term. There are various fields that theoretical physicists have played with: chameleon fields and phantom fields and quintessence and such. The difference to the cosmological constant is that these fields’ densities do change with time, albeit slowly. There is however presently no evidence that this is the case.
As to the question which dark stuff to include in which term. Dark matter is usually assumed to be pressureless, which means that for what its gravitational pull is concerned it behaves just like normal matter. Dark energy, in contrast, has negative pressure and does odd things. That’s why they are usually collected in different terms.
Why don’t you normally read about dark energy being made of particles? Because you need some really strange stuff to get something that behaves like dark energy. You can’t make it out of any kind of particle that we know – this would either give you a matter term or a radiation term, neither of which does what dark energy needs to do.
If dark energy was some kind of field, or some kind of condensate, then it would be made of something else. In that case its density might indeed also vary from one place to the next and we might be able to detect the presence of that field in some way. Again though, there isn’t presently any evidence for that.
Thanks for your interesting questions!

Thank you for this. I had forgotten/misunderstood the negative pressure aspect of the cosmological constant term so this helps distinguish the darknesses (for me, at least). As a follow up for the future, if time becomes available, I'd like to inquire about this paragraph:
ReplyDelete"Since the cosmological constant is also present if matter sources are absent, it can be interpreted as the energy-density and pressure of the vacuum. Indeed, one can calculate such a term in quantum field theory, just that the result is infamously 120 orders of magnitude too large. But that’s a different story and shall be told another time..."
There is this paper by Fields: https://arxiv.org/abs/1502.03424 which, if I understand -- which I doubt, frankly -- sources dark energy via Landauer's principle to the precision with which we map the position of galaxies, etc. The 120 orders of magnitude shows up here as well.
When you discuss the vacuum energy density calculations from QFT eventually, I would be interested in your comments on this paper (if it's worth consideration). Thanks again.
Very nice explanations!
ReplyDeleteHi Sabine,
ReplyDeletethanks for a very interesting post.
First let me ask a naive question I was asked some time ago: space-time expands. OK, in what? (I know it is not so simple.)
As for the main reasoning, using Noether's theorem is fine, but as always a theorem does not say more than its premises - so energy conservation is "already" part of those premises. Perhaps that's where to look.
Last, my main question. I understand quantum gravity should give us at least a feeling about the big bang (maybe even an explanation), so what about energy creation? Why should it be big-banguesque? Why not a permanent creation? (and a small "pshit" to begin with).
Best,
J.
"If dark matter was some kind of field, or some kind of condensate, then it would be made of something else. In that case its density might indeed also vary from one place to the next and we might be able to detect the presence of that field in some way. Again though, there isn’t presently any evidence for that."
ReplyDeleteI could be misunderstanding.. but did you mean dark energy instead of dark matter?
akidbelle,
ReplyDeleteIf you do cosmology, you make a space-time split and you chose certain coordinates on that space and in these coordinates space expands. Period. It doesn't expand into anything, it just expands. You can chose coordinates in which it doesn't expand, but these are awkward because they mix space and time and are difficult to interpret.
The major problem many people have with GR who don't use the math is that they think of curvature as something that is defined through the embedding of a space (or space-time), but that's not the type of curvature one uses in GR. It's an intrinsic property of space-time, not a property of an embedding.
Now you can take any 4-dimensional space and embed it into a 10 dimensional space, and then you could say it expands 'into' that larger space. But that's an interpretation nobody uses, at least not that I know of.
Of course you use stress-energy conservation already to derive the equations. I was just explaining how it's connected to the space-time symmetries.
Re your question about quantum gravity, nobody knows and I don't know either. Best,
B.
Unknown,
ReplyDeleteThanks for pointing out, I've fixed that!
Thank you again, Dr. Hossenfelder, for your insights concerning these puzzling aspects of our universe.
ReplyDeleteEinstein was careful to ensure that the left-hand side of his field equations (G) had zero divergence, so that they would match the conservation condition for the energy-momentum tensor T. But if energy-momentum is not strictly conserved for an expanding universe, then I still have to wonder why we impose it in the first place. Is zero divergence more a required mathematical condition than a physical requirement?
Bill,
ReplyDeleteT (right hand side) is covariantly conserved, as I said. That's the criterion Einstein used. From that requirement you know that the left hand side must be a certain combination of the Ricci tensor and the curvature. (Basically, it fixes the factor 1/2). It's the same condition that I'm talking about. Best,
B.
"the equivalence principle...the requirement that the equations be tensor-equations" OK, but achiral spacetime curvature prohibits Sarkharov conditions, a matter-excess universe. Add chiral (think "Lorentz force") parts-per-billion spacetime torsion. Spacetime mirror symmetry relaxes toward fermion quarks. Conservations (Sakharov, dark matter) relax in reduced symmetry media (Born scattering approximation, Fermi's golden rule, Snell's law).
ReplyDeleteTrace chiral vacuum background is quantitatively validated at least six different ways using chemistry. Look
fluid with constant density and with constant, negative pressure Close-packed glass microballs’ void spaces (26 volume-%, [1 - (pi)/3√2]) are water. Hydrophilic surfaces plus curvature (capillary action) sum to large positive pressure. Silanize the surfaces hydrophobic or use mercury (capillary depression), obtaining large negative pressure.
http://video.nano.msu.ru/nano/Images/Terms/capillar.jpg
http://www.solitaryroad.com/c1023.html
https://en.wikipedia.org/wiki/Kelvin_equation
Planck volumes? Repulsion.
Thank you Sabine, great post again:)
ReplyDeleteHere might be another similar typo or my misunderstanding(?) in the last line above the last paragraph:
"... neither of which does what dark matter needs to do. "
Do you mean dark energy here as well?
Another question on the equivalence principle – Why does gravitation obey the principle? In Weinberg's 1971 book on the subject, he thought that the answer would not be found in the realm of classical physics, but perhaps in the quantum world. Any thoughts?
ReplyDeleteDear Dr. Sabine,
ReplyDeleteThank you for another interesting post.
My question is kind of delicate, so I understand if you choose to ignore it.
I have puzzled over many comments published by "Uncle Al", which to me are mostly baffling. I keep hoping you will address one of them, but I have not seen you do it yet. So I am wondering if you ever make sense of what he is saying?
My apologies if my question is inappropriate.
Best, Henry
Henry,
ReplyDeleteI rarely address Uncle Al. To the extent that I can make sense of what he writes, he's been writing the same since 10 years. He's basically part of the family, which is why I often approve a post or two. For all I can tell he has never trolled anyone and he doesn't post extensively either. So. You know, he's like that crazy uncle you have who'll sit on the couch and talk about penguins every time he stops by, and you can't make sense of it but you don't want to throw him out either, so you make him a tea and let him talk. Best,
B.
joy who isn't,
ReplyDeleteThanks, I've fixed that. Sorry for the confusion!
Robert,
ReplyDeleteThe equivalence principle is primary. It's a postulate. Or mathematicians would call it an axiom. You can't construct theories from nothing, and that's one of the starting points. What you can do is to reformulate it in other ways, eg by saying that gravity couples universally or just by writing down an action, or principles you allow for terms in that action. But it always comes down to it being postulated. Best,
B.
hmm.. I've always disliked postulates. I'm still waiting for someone to explain the invariance of light speed!! But seriously, I would expect that if we ever understand quantum gravity, perhaps we will also have a better understanding of the physics underlying the EP.
ReplyDeleteHi Bee! Penguins do not fly - except underwater, where they marvelously do. I'll email you (Frankfurt Institute) a picture of the apparatus held between two fingers. Their 1999 considered chiral test masses were mirror image machine screws. Usch då Right idea, wrong scale, and not self-similar all the way down. Somebody should be lining a bird cage empirically, not in theory. Do the experiment.
ReplyDeletehttps://www.youtube.com/watch?v=XZm6y0ALDCc
Optimize everything.
Bee, you are confusing the invariance of the universe with the invariance of the equations of motion. Noether's theorem for energy applies when the equations of motion are invariant. This holds in general relativity so energy really is conserved. The fact that the universe itself is changing has no bearing on this. The expansion of space is just change in the metric, i.e. the gravitational field. If this spoilt energy conservation, the same argument would apply to any other field changing. There would be no energy conservation in electromagnetism because the electromagnetic field changes for example. This is obviously nonsense and the error is to confuse invariance of the equations of motion with the invariance of the solution. Why do people make this mistake in GR but not in other field theories?
ReplyDeleteWhat actually happens with the cosmological constant as dark energy is that the dark energy is increasing, but it is balanced by a negative term for energy in the gravitational field due to the accelerating expansion. This is described by the Friedmann equations in the case of the standard cosmological model. It may sound like an odd explanation but it is exactly what Noether's theorem gives if you work through all the details properly.
Just now there is a Nature Science Report (OA) by Sarkar et al. stating that the 2011 Nobel result shrinks below 3sigmas when a ten times larger sample is used.
ReplyDeleteHow much dark energy is really needed?
"You can for example take the term with the cosmological constant and not think of it as geometrical, but instead move it to the other side of the equation and think of it as some stuff that causes curvature"
ReplyDeleteNot being deliberately obtuse but how so from a term which goes to the other side multiplied by -1 is all
But the inverse you envisioned...is it original to you?
I was wondering what you thougt of the new paper questioning the accelerating expansion of the universe.
ReplyDeletePhilG,
ReplyDeleteNoether's theorem is a statement about symmetries acting on the Lagrangian. If space-time enters the Lagrangian then its symmetries (or absence thereof) matter. As to the rest of your statement, well, it's just wrong. If you don't believe me, look it up in a textbook. Best,
B.
piein,
ReplyDeleteI don't know what you mean. I'm just saying you can write this term on either side. Look, the terms with the R's in them are clearly geometric. The terms with matter-fields in them are clearly sources. The term with Lambda, you can either interpret as geometric or as some matter thing. But really, this is just words, the equation, needless to say, remains the same. I don't know what 'inverse I envisioned' but all I've explained in this post is very standard knowledge. Best,
B.
Sabine,
ReplyDeleteI wonder if the equation could be considered fully geometrical, because linking the source terms with geometry seems incomplete. At the bottom of particles physics, the source terms are usually called "resonances", waves, matter-wave, all that which is embedded in the SM or older theories. So the micro-stuff looks geometrical.
@Thierry Pierrat,
thanks, I wonder if you realize that a small "pchit" means that the "previous" state is certainly not about energy. Basically, I think that physics is stuck with this: there is a constant of action, no constant of energy - but still energy is quantized in the form of mass (massive particles). The bottom-line is not energy, it is action. Dead lock! But the "right" question may be to understand what energy is.
So, what I wrote is not creationism, but energy production. Even though this is just words I guess this would be a nightmare for physicists.
Best,
J.
Bee, If the spacetime metric is treated as a background field in the Lagrangian then it's symmetries will matter, but spacetime is also dynamic and should not be treated as a background field. If you don't treat it as dynamic then you are not taking into account the energy in the gravitational field so of course energy will not be conserved. This works the same with any other field theory. For example, if you treat the electromagnetic field as a background field then you can only derive energy conservation if the field is static because in the real world energy passes between charged particles and the elctromagnetic field. This also happens with gravity. If it didn't they would not have detected gravitational waves at LIGO.
ReplyDeleteAs for your patronising comment about looking it up in a textbook please give me an example. Treatment of energy conservation in the GR textbooks is very patchy but Dirac, Weinberg, Landau & Lifshitz and Einstein would agree with me.
PhilG,
ReplyDeleteYou talk down at me and when I tell you what I wrote is textbook knowledge that's supposedly "patronizing"? Yes, you can interpret the local conservation law in GR as taking into account the dynamics of the background. But there isn't (in general) any such thing as the energy of the gravitational field (though you can define one in special circumstances). You find the formal version of my above statements eg in Weinberg's textbook, section 5.3 (page 127), which is all I meant to say. Best,
B.
Hello Sabine,
ReplyDeleteOn that energy of the gravitational field.
Doesn't it make sense - given the equivalence between inertial and gravitational mass - that the gravitational field holds energy ?
Because an input of energy causes energy absorption of mass in flat spacetime (acceleration) according to E=ymc2 (sorry for bad formulation here). This would imply that an accelerating mass in curved spacetime absorbs energy that was already there.
What do you think ?
Koen,
ReplyDeleteEnergy is not a local quantity. It's an integrated quantity. Look at the field equations I have in the post. The source is T_munu, that's the stress-energy tensor. Energy is NOT an entry in this tensor. Instead, it's energy-density. Hence, I don't even know what you are talking about.
B.
Sabine,
ReplyDeleteI understand what you say, but it also raises eyebrowes. Explanation here for instance (Weiss & Baez) :
http://math.ucr.edu/home/baez/physics/Relativity/GR/energy_gr.html
Especially the assumption that 'gravitational energy' does not act as a source of gravity. It goes against the equivalence principle in my opinion. Since in the inertial case, you genuinly add energy to cause acceleration. So in the gravitational equivalent, you can't be pulling it out of an empty hat, to cause acceleration.
The key here is to understand that for instance the matter energy of the earth is what causes the necessary energy of the gravitational field (matter curves spacetime) in order to make your applre accelerate (fall to earth).
Concluding thus that curvature of spacetime, is only our current way of expressing this gradual energy level radially outward. And the precise configuration of it, becomes part of the subject for the as yet inexistent theory of quantum gravity.
I firmly hold on to full respect for the equivalence principle here.
What do you think ?
P.S. You might now also have a path of investigation to find your missing dark energy locally, as source of a static pre-expanded space, instead of an ever expanding space.
As a change in assumptions is usefull if it solves current issues while not conflicting with experimental evidence.
Best, Koen
Dear Bee, I am not sure how I am supposed to disagree with you without you thinking I am talking down to you. That was not my intention. In any case, Weinberg gives the full treatment of energy conservation including the energy in the gravitational field on page 165, section 7.6 For the case of expanding cosmology turn to page section 15.1 page 472 but this would need to be updated to include the cosmological constant which is only discussed at the end on page 615
ReplyDelete@Thierry Periat,
ReplyDeleteagreed of course; though action (= energy x time) is firstly connected to the existence of a quantum of action and of angular momentum, which is a much more basic mystery - I think.
J.
PhilG,
ReplyDeleteI'm sorry in case I was too harsh. Read the first sentence of section 7.6, it's not a covariant treatment. Same for FRW - preferred background. The covariant conservation law is the local one. As I said already above, there are certain situations in which you can define reasonably meaningful quantities, which are the cases you seem to be referring to.
Thierry,
ReplyDelete“Does the relation volume x volumetric density of energy = energy not hold true for the cosmological constant?”
Spatial volume isn't uniquely defined in general relativity. Volume in which coordinates? You can define energy this way in FRW if you wish (preferred coordinates). Then that energy won't be constant. (Volume increases, density stays the same.)
And “What if that some kind of stuff we actually don’t know would be a kind of perfect fluid?”
Yes, what if? Sorry, can't parse the question. Best,
B.
Koen,
ReplyDeleteThere isn't any such thing as gravitational energy (in general). The closest you can get to making sense of gravity gravitating is graviton self-coupling, but that again relies on using perturbations around some fixed background. Really, you have to stop thinking of gravity in terms of potential and energy. It's a property of space. Best,
B.
Sabine,
ReplyDeleteUnify units of space with units of energy, and you can still respect that equivalence principle. And at the same time you are replacing the continuum with a discontinuum, to match better with the discontinuum of matter.
Gravity will remain a property of space, while space now entails a local configuration of energy.
(Following up on Sakharov's concept of space responding to the presence of matter). Absorbing energy,due to action-reaction. It is also a basis of research in emergent gravity (T. Padhmanaban etc).
Best, Koen
Bee, there are covariant formulations of energy in general relativity that include the energy of the gravitational field, but the textbooks have not covered this well. The Komar superpotential is a good starting point. The non-covariant methods are not wrong though. Energy in GR depends on the frame of reference just as it does in SR, but in a more complex way. Conservation laws are expressed in the representation dual to the symmetry they are related too by Noether's theorem, and for the diffeomorphism group the dual representation does not reduce to a stand-alone tensor field representation. This means the energy current needs to be written explicitly as a function of the vector field specifying the diffeomorphism. You see this in the expression for the Komar superpotential which has a dependence on a vector field. This is not a problem, it just means you have to select a coordinate system (more specifically a time translation) before making meaningful measurements, but that is true for any observable quantity anyway.
ReplyDeleteIn the case of the standard cosmology you can choose any time translation you like to determine your energy equation. Of course it is most natural to choose the standard time coordinate used in the cosmological model which then gives the Friedmann energy equation. You may then complain that it has a preferred background, but of course it must since you have chosen a specific frame of reference for simplicity to reduce the equations to something you can use. This is not a weakness of the energy conservation law.
PhilG,
ReplyDeleteI don't know if that's a convulated way to agree with me, but I certainly hope so. Yes, there are ways in which you can define some current by picking a vector field and so on. I don't know how this is in contradiction with what I wrote. All I've said is that if you don't have translational invariance in space and/or time, then there are no conserved quantities related to that symmetry. Yes, there are other ways to define other quantities, nobody disagrees on this. Honestly, I get the impression you are just looking for some opportunity to tell everyone you know something.
I never said that picking a preferred frame is a "weakness" or that there's something wrong with that, so please stop putting things into my mouth just to find something to disagree with. At this point I am pretty sure you know exactly what I mean. Best,
B.
Bee, I still disagree with your statement that there are no energy conservation laws when the spacetime does not have time translation invariance. I have given my reasoning for that. You brought up the subject of non-covariance and preferred reference frames so I am saying some things about those too.
ReplyDeleteYou said "I never said that picking a preferred frame is a "weakness" or that there's something wrong with that" Likewise I never said that you said that it was a weakness, I was just pointing out that it isn't in case anyone thinks it is.
You say "I get the impression you are just looking for some opportunity to tell everyone you know something." Why can I not say the same thing about every blog post and comment you ever wrote? What I am actually trying to do is dispel the myth of energy non-conservation in general relativity.
I think you need to stop using these defensive meta-arguments and answer the scientific points I made instead.
PhilG,
ReplyDeleteLet me put it this way: I think we both agree on the math. We've read the same textbooks. You seem to understand what I'm saying, I understand what you're saying, or at least I think so. Yes, I do make mistakes, but this isn't one of them. Read again what I wrote - at this point you're not even commenting on that any more, you're just trying to comment on something. What you don't understand is that if you erroneously complain something I wrote for my blog readers is wrong, you're undermining the trust they have in me, and I'll have to explain publicly just why what I wrote is perfectly correct. You'll get a full-blown defense, and I don't like that either because it wastes my time.
Look, I'm trying very hard to get across concepts of theoretical physics that are obvious to those in the field but that are still mysterious to the rest of the world population. Read for example Koenraad's comments to see what I mean. Got an impression? Now you stomp into the kitchen and complain that something rather basic which I wrote is wrong, something that's arguably oversimplified but that I still think people should at least be able to grasp. Who do you think is helped by your comment?
You asked me above how you can disagree with me without talking down at me. To begin with you shouldn't complain something I wrote is wrong when it's right, especially after I explicitly told you exactly what formal statement I have referred to, including section and pagenumber. Had you just posted a comment that said: Oh by the way, you can alternatively also do X, and in the case Y also Z, we'd never have had this exchange.
So let me just make a suggestion then. Why don't you repost your comment in a less offensive way and just explain that there have been various proposals to recover a concept of energy in GR, and what are their advantages and disadvantages if you wish, and I won't have to disagree with that.
Best,
B.
Koenraad,
ReplyDeleteSorry, I can't make sense of that.
PhilG, I'm a little confused of what you are you trying to convey here, so before we reinvent the wheel can you tell me if you agree with the following statement which I think is the conventional wisdom:
ReplyDeleteIf you want to take into account the energy of the gravitational field then the only well defined notion of total energy conversation in GR (full-fledged with no background metric) is a global one and only for asymptotic flat space-times.
Sabine,
ReplyDeleteThe problem I was trying to point out: following through with the equivalence principle should lead to gravitational energy,hence gravitational mass increase when getting closer to a potential well. Because we do have an inertial equivalent.
T
A directly related issue is recognized by physicists in the form of the problematic formulation of mass in GR as indicated in the link below.
"The main reason for this is that "gravitational field energy" is not a part of the energy–momentum tensor; instead, what might be identified as the contribution of the gravitational field to a total energy is part of the Einstein tensor on the other side of Einstein's equation (and, as such, a consequence of these equations' non-linearity). - etc "
https://en.wikipedia.org/wiki/Mass_in_general_relativity?wprov=sfla1
Add to that that we have a 95% mystery concerning concepts of dark matter and dark energy.
So suggesting that those 2 issues are related and working towards a different interpretation than that of the current theory, can be valuable.
Best, Koenraad
Koenraad,
ReplyDeleteYou write
"The problem I was trying to point out: following through with the equivalence principle should lead to gravitational energy..."
No, it doesn't. I don't know why you think it should, but it doesn't. If you can't follow the math, I'm afraid you'll have to trust me on that. Best,
B.
I make no apology for undermining your reader's trust. Science should not be taken on trust. Nobody is always right, not you, me, Weinberg or anyone else. I count myself fortunate in that people do not trust me. I am not associated with a respectable academic body and I go against the system, so if I get a point across it is because I made a good case. There is nothing less satisfying than to be taken on trust.
ReplyDeleteLet me quote from your post
"In a curved space-time generically neither symmetry is fulfilled, hence neither energy nor momentum are conserved. So, if you take the vacuum energy density and you integrate it over some volume to get an energy, then the total energy grows with the volume indeed. It’s just not conserved. How strange! But that makes perfect sense: It’s not conserved because space expands and hence we have no invariance in time. Consequently, there’s no conserved quantity for invariance in time."
This is wrong. There is no way of saying that which is more polite. If I surround it with platitudes people will think I am unsure about it.
The reason it is wrong is because it confuses the invariance of the spacetime solution with the invariance of the dynamical equations. Noether's theorem applies to the latter. If you invoke the invariance of the spacetime metric itself then you are treating spacetime geometry as a background field. You are then ignoring the changing energy in the gravitational field itself. You then think that energy is "just not conserved" but that is wrong. When the energy of the gravitational field is included then the energy is conserved.
Weinberg gives one treatment of energy in the gravitational field which works. You pointed out that it is not covariant but I think we agree that it is still valid and that there are other approaches that are covariant. Why then do you still say that energy is "just not conserved" ?
Perhaps it would help if I give some background context. A long while back I was editor of the Physics FAQ and contributed a number of articles to it. One of the articles I did not write was about energy conservation is GR. The article by Baez and Weiss is inconclusive. It is often cited in support of non-conservation but it says nothing of the sort. I was not satisfied with this so I undertook to investigate the situation more fully.
The history goes back to Hilbert against Einstein and a long debate about whether gravitational waves can carry energy. It's not easy to figure it out. People use all kinds of arguments to explain why energy conservation does not work. Famous relativitists and cosmologists such as Wheeler and Peebles have accepted some of these arguments and written them in to textbooks, but they are all spurious. You can do the math and the math does not lie. Noether's theorem works. Energy is conserved. I think you are capable of understanding this so please ignore what you have been told and take a fresh look at it.
If you don't trust me well enough and need to trust someone else before you will reconsider, then read what Guth has to say about energy conservation in inflation at http://www.counterbalance.org/cq-guth/howdo-frame.html He explains that energy is conserved during inflation because of the negative contribution from gravitational energy balancing the poistive contribution of the inflaton field. The same principle works with the cosmological constant at a lower scale. Do you agree?
Giotis,
ReplyDeleteI don't quite agree that the only well defined notion of total energy is for asymptotically flat spacetimes. There is also a well defined notion of total energy for a finite closed universe. Of course we should not expect a well defined notion of total energy in a universe with an infinite amount of matter.
The more general formulation of energy conservation is in terms of an energy current four vector with an explicit dependency on the time translation vector field. If it's 4-divergence is zero then it can be integrated over a volume of space to give an energy for that region which changes at a rate given by an integrated flux term over the boundary of the region.
PhilG,
ReplyDeleteNo, you are misreading what I said, and given that I already explained above that I am referring to the symmetries of the Lagrangian and explicitly told you the exact equations which I am referring to, I can at this point only conclude that you are deliberately misreading me.
Yes, as I already agreed above, you can in certain situations or with certain additional assumptions come up with alternative notions of energy, other than the conserved current related to time-invariance. But if it's not covariant, it's not generally valid, and if you define it by a measurement procedure, then it depends on that procedure. I don't know why you bring up the Guth argument, that's a space with lots of additional symmetries and also nobody doubts that there are ways to define gravitational potentials or gravitational energy in certain circumstances with certain properties. Best,
B.
Gravitational energy is not something that can only be defined in "certain circumstances." The treatment is general, and as I said earlier, if you don't like the non-covariant formulations like the one in Weinberg you can use Komar's highly cited formulation http://journals.aps.org/pr/abstract/10.1103/PhysRev.113.934
ReplyDeletePhilG,
ReplyDeleteWell, you can of course just define something and insist on calling it gravitational energy. Whether that's meaningful is another question entirely. On the same reasoning, you can of course make any quantity that you define in one coordinate system generally covariant by defining the same quantity in all other coordinate systems to be the suitably transformed quantity. If I recall correctly, Komar already pointed out these shortcomings, so let me just quote this straight from the paper you refer to
"We can continue to recognize the conserved quantity in other coordinate systems, but the identification with energy or momentum may no longer be as reasonable."
Also, note that he very openly states:
"we have considered imposing certain natural covariant conditions on the vector fields which we choose to identify with energy and momentum"
(Emphasis mine).
A lot of further work has been done since Komar wrote his paper. The expression he came up with is not just something you define and "insist on calling it energy." It can be derived from Noether's theorem. It can be integrated up to give the ADM energy for an isolated system. It gives the right energy for gravitational radiation as confirmed experimentally for binary pulsars.
ReplyDeleteIt is also given by an explicitly covariant expression. I dont think it is consistent to argue on the one hand that quantities need to be covariant to be "generally valid" and then say that you can make any quantity generally covariant by some trick. Where does that leave you?
PhilG,
ReplyDeleteWhere does that leave me? That was a question addressed at you. You say, here you can do it. I say it's not covariant. You say, I can make it covariant. I say, well, you can make anything covariant if you throw out the interpretation. What's inconsistent about me pointing out you're not making sense?
Yes, ADM for isolated systems (special case), gravitational radiation (special case). Really, I am getting tired of this. You know exactly what I referred to in my post. I've explained it often enough. Yet you insist there must be something wrong with it because people have studied alternative ways to define what energy means. As I have now told you half a dozen times, nobody doubts that.
Allow me to summaries then. There is a completely general formulation for energy conservation in general relativity that takes into account the energy in the gravitational field. It reduces to sensible answers in all special cases including the cosmological context of dark energy which is the subject of your post. It can be derived from the time invariance of the dynamical equations in the full theory via Noether's theorem. It has a natural covariant form, and is not arbitrary or trivial in any way. It even agrees with experimental observations of gravitational waves. By the way it is also perfectly in line with and analogous to the derivation of familiar conservation laws for other gauge theories. As far as I can tell you do not dispute any of this but you still insist that in some sense energy is "just not conserved."
ReplyDeleteI am just a bystander in this somewhat stormy discussion between Dr. Hossenfelder and PhilG. But it seems to me that Sabine, who is gracious enough to entertain this argument on the blog that she owns and administers, deserves to know something about her adversary's credentials since her credentials as a renowned physicist are well known to everyone here.
ReplyDeletePhilG, yes but this is already an isolated system so let's forget Cosmology for a moment, I'm talking about GR as a theory here.
ReplyDeleteIn GR you can define the gravitational energy only globally in an isolated system; the way people isolate systems is by putting them in an asymptotically flat space-time. Only then you can define the notion of total energy that can be only globally conserved.
In GR there is no notion of total (matter + gravitational field) locally conserved energy.
But this is textbook stuff, so I guess you don't disagree;
So I really don't understand what are you are trying to say.
Can you formulate your disagreement in a simple statement?
Everyone seems to write the field equations in either fully covariant or fully contravariant form. I always write them in mixed form simply because then the metric tensor is simply the unit tensor. Am I missing something?
ReplyDeleteI'm trying to understand your point of view which you think should be clear to me. So I said that treating the spacetime metric as a background is a bug that leads to a non-conserved energy because it neglects gravitational energy, and that there is a better way to do it where energy is conserved. However, your argument is that anyone is free to extend the definition of energy in any way they want, so the bug is a feature in your definition of non-conserved energy which I should accept as equally valid?
ReplyDeletePhilG,
ReplyDeleteI don't know how you want to derive a conserved current from time-invariance if the Lagrangian in general isn't time-invariant. I don't know what you mean by talking about Noether's theorem referring to the dynamical equations, I know Noether's theorem from the Lagrangian treatment. I have no idea why you think I want to keep a background fixed.
What I object on is your insistence that there's a 'general' notion of graviational energy. I don't disagree that you can define one more or less meaningfully in certain context.
My point of view, I am afraid to inform you, is the rather boring textbook view. General Relativity is a local theory. There isn't any such thing as energy in this theory, there is the stress-energy-tensor and it contains densities. Once you start constructing integrated quantities, which is what you need to do to get something you can call an energy, you necessarily have to bring in additional assumptions. If you have situations with additional symmetries, these can provide additional assumptions. If you use small perturbations around a fixed background, these background brings in additional assumptions. If you refer to certain classes of observers, these can provide additional assumptions.
But in general, what you have in GR, is a local, covariant, conservation law for the stress-energy-tensor. And that's it.
Best,
B.
Bee, I am sorry I have not been able to successfully explain my point about why your approach is incomplete. I can only hope that some others have understood it. As for the textbooks, many of them do not cover energy conservation, some deal with only special cases, a few get it wrong, but others such as Weinberg give a complete and satisfactory (albiet outdated) treatment of energy concentration for the general case which includes the gravitational energy. The idea that energy conservation is somehow deficient is more of an internet meme than a textbook fact.
ReplyDeleteHi Sabine,
ReplyDeleteHave you already read this recent article http://www.nature.com/articles/srep35596, where the authors, "using the JLA catalogue of 740 SN Ia processed by the SALT2 method","find marginal (i.e. ≤ 3σ) evidence for the widely accepted claim that the expansion of the universe is presently accelerating".
Yves,
ReplyDeleteYes, I have seen it. The only reason I'm posting your comment is that you're like the 20th person who wants to tell me about this. (I didn't post the other comments.) I appreciate your concern about my timeliness, but I don't live under a rock. I just don't think it's my task to comment on any news item that has something to do with physics. Also, I don't find it very interesting. It's quite common for measures of statistical significance to change either way when new data is taken into account. And it's not like they find an actual incompatibility with other data sets. (And even if they did, as they say, extraordinary claims require extraordinary evidence.) All this is just to say, I'll not write a post about it, in case that was the question. Best,
B.
Doc HOssenfelder says: " I don't know what 'inverse I envisioned' but all I've explained in this post is very standard knowledge"
ReplyDeleteWell...what was the dependence between the alternate interpretation, and the rearrangement of the equation resulting in the term going to the other side?
piein,
ReplyDeleteSame equation, different interpretation.
This discussion reminds me of a similar one on Sean Carroll's blog:
ReplyDeletehttps://www.preposterousuniverse.com/blog/2010/02/22/energy-is-not-conserved/
PhilG, I will interpret the fact that you didn't respond to my comment as an implicit agreement.
ReplyDeleteThat being said I read the post and Bee's statement that:
"But General Relativity has a more complicated type of symmetry to which Noether’s theorem can be applied. This gives rise to a local conservation of stress-momentum when coupled to gravity (the stress-momentum tensor is covariantly conserved). "
is not quite correct either in the strict sense.
The stress-energy you take if you apply Noether's theorem to Einstein Hilbert action (known as canonical energy momentum tensor) is not the stress-energy tensor that appears in the Einstein equations.
Personally I wouldn't even mention the word Noether around GR but that's just me:)
Giotis,
ReplyDeleteYes, indeed! And that's a very interesting point about which I wrote a paper a long time ago... But maybe somewhat too much detail for the purposes of this post.
Giotis, Sorry I did not respond before but you are saying the same as Bee and I have already responded at length to her.
ReplyDeleteNo I don't agree with your statement that "In GR there is no notion of total (matter + gravitational field) locally conserved energy." Not all textbooks cover this but Weinberg gives one such formulation which I have cited. Komar wrote a paper giving a covariant formulation. If you say that your statement is textbook stuff then it would help to provide a specific textbook reference that explicitly states something close to what you are saying so that I can see where you are getting it from and respond to it. Alternatively you could give your own justification. Actually this subject is still not covered well in the textbooks. As I said to Bee, the belief that there is something deficient in the law of conservation of energy in GR is more of an internet meme than a textbook fact.
I am surprised that you do not want to mention Noether in the context of GR. Noether's theorem applies perfectly in GR. In fact Noether studied it originally to understand conservation laws in GR shortly after Einstein gave his solution.
Found it... and as I was expecting my statements were correct.
ReplyDeleteMy friend Wald will save the day once again :)
If you want textbook references, here it goes:
Wald, page 70, note 6:
"One might hope to recover an energy conversation law by including the stress-energy of the gravitational field as it is done in Newtonian theory. However in General Relativity there is no meaningful local expression for gravitational stress-energy and thus there is no meaningful local conservation law which leads to a statement of energy conservation. Nevertheless as will be discussed in chapter 11, a conserved total energy of an isolated system can be defined even though there is no local expression for energy density."
Winning:)
Giotis, I am aware of Wald's view but I dispute it. Notice that he gives no detailed justification for his claim and he also inserts the weasel word "meaningful". What does he mean by that word and why does he consider it necessary to insert it? Why is the formulation provided by Weinberg not meaningful? If he means that it is not covariant (and I disagree that this makes it not meaningful) then what is his objection to Komar's local expression which he uses himself in the book?
ReplyDeletePhil,
ReplyDeleteIt is well justified in other places e.g. page 84
Komar is for static asymptotically flat space-times. Check page 289.
Weinberg is not full-fledged GR, not covariant, he splits the metric and asymptotically flat
I really can't understand why you keep defending an indefensible position.
Giotis, Wald's statements about energy are completely without merit. He just makes claims about how you can't divide the metric into background and dynamical parts and complains that formulations are not covariant and are therefore meaningless. He also worries about non-uniqueness of the energy formulism. Einstein, Dirac, Landau and Lifschitz and Weinberg understood that these methods work and applied them to gravitational waves in ways which could be experimentally verified. Just stating that something cannot work does not make it true. He needs to give a real physical reason, and he does not do so.
ReplyDeleteI don't think this forum is conducive to continuing this discussion given the moderation delay and the lack of support for maths equations which would be needed to pursue this further.
PhilG,
ReplyDelete"Just stating that something cannot work does not make it true. He needs to give a real physical reason"
It's because of the equivalence principle. The Misner-Thorne-Wheeler book, Chapter 20, sections 20.3 and 20.4, elaborates why and provides the physical reason. The punchline is in the second-to-last paragraph of 20.4:
"At issue is not the existence of gravitational energy, but the localizability of gravitational energy. It is not localizable. The equivalence principle forbids."
The sections 20.3 and 20.4 explain in detail why this is so, and the last paragraph of 20.4 does so on the vivid potato-example:
"Look at the small region of the surface of the potato. The geometry there is locally flat. [...] In an appropriate coordinate system it is free of gravitational field. The over-all effect one is looking at is a global effect, not a local effect. [...] That is the lesson of the nonuniqueness of the [gravitational stress-energy pseudotensor]."
I recommend those chapters in the MTW book, it's a good read.
Also, you should know that Emmy Noether actually proved *two* theorems about the conservation laws. The first explains how the existence of a global symmetry gives rise to conserved quantities. The second explains how the existence of a local symmetry *does not* give rise to any conserved quantity, but instead to appropriate Bianchi identities. Given that in GR a generic spacetime configuration does not have any Killing vectors, there are no global symmetries (except in special cases), and therefore the first Noether theorem is void --- there are no conserved quantities like energy or momentum. Moreover, given that GR has a local Poincare symmetry, the second Noether theorem gives rise to Bianchi identities, which imply the covariant conservation of the matter stress-energy. Couple that to the nonuniqueness of the gravitational stress-energy (courtesy of the equivalence principle), and conclude that the notion of the "total" matter+gravity stress-energy is neither definable, nor gives rise to any integral conserved notion of energy (or momentum, or angular momentum for that matter). That's why the Landau-Lifschitz pseudotensor has the word "pseudo" in it. And L&L did acknowledge this in the second volume of their opus (section 96, paragraph below equation (96.14) in the fourth revised English edition).
I dare say that Weinberg's book is not really the best textbook out there, to learn GR from.
HTH, :-)
Marko
It's not just Wald, there isn't a single textbook that defends your position.
ReplyDeleteCheck Misner et al beautiful analysis.
page 466 under Chapter with title:
20.4. WHY THE ENERGY OF THE GRAVITATIONAL FIELD CANNOT BE LOCALIZED
It can only be understood globally as total energy and only then you can speak about energy conversation in a meaningful way
There you will also find the physical reason you are asking for.
Anyway I give up 'Gravitation' is a very heavy book to carry around, LOL
Yes, the stubbornness of the moderator to keep on this comment policy is unexplainable.
ReplyDeleteNo one else does that, it kills any kind of sensible discussion.
Not even juntas do this kind of censorship
Giotis,
ReplyDeleteI am sincerely sorry about the moderation delay, but dark matter/energy is a topic that attracts a ridiculous amount of crank theories and, trust me, if I'd post them all, that wouldn't benefit this comment section. It's easier to approve the reasonable comments than to later delete the useless ones. In any case, thanks for your effort with PhilG.
I dont blame Bee for moderating, just saying it slows down the debate. I'm glad she has been willing to allow my very direct comments.
ReplyDeleteMTW is one of the textbooks that initiated the myth that there is no local formulation of energy conservation. In earlier work Wheeler even claimed that the energy conservation law was a trivial result because it gave a value of zero for a closed universe. Again it can be shown that it is not trivial. Like many of the arguments used against energy conservation it can be shown that the same arguments could be applied equally well to conservation of charges in other gauge theories, yet the conservation laws are accepted as valid in those cases.
Again it is not true that no textbook defends my position. Weinberg is an example of a book which covers energy conservation without noting any issues.
Bee is not simply slowing down the debate. She is granting her mercy to a dead horse.
ReplyDeleteDear Sabine,
ReplyDeleteYou wrote: "Now you can take any 4-dimensional space and embed it into a 10 dimensional space, and then you could say it expands 'into' that larger space. But that's an interpretation nobody uses, at least not that I know of."
What are the pitfalls of that interpretation? Are the efforts of AdS/CFT trying to move in that direction (but with quite a few more dimensions to get to 10, i suppose)?
Thank you for your space-time!
just zis,
ReplyDeleteI don't know if there are any pitfalls, but you know how it goes with interpretations, once one becomes widely spread, it takes over. It's like with the Copenhagen interpretation. Could have been some other one, but it just wasn't. The way it went historically is that Einstein's whole motivation was to come up with an internal measure for curvature, so naturally there isn't any embedding space.
No, this has nothing whatsoever to do with AdS/CFT or (super) string theory. I know the number-match suggests it might mean something, but not that I've been able to see at least. The number of the maximal embedding space is simply (d)(d+1)/2, that's the number of independent entries of the metric tensor in d dimensions. For d=4, that happens to be 10. If you have symmetric spaces, fewer will do. I've certainly seen more interesting numerical coincidences than that. (Here's one: Did you know that the surface of the unit sphere is maximal for 7 dimensions?) Best,
B.
Although 10 dimensions is sufficient to embed a 4 dimensional manifold locally (i.e. in a sufficiently small neighbourhood), it is not sufficient globally. For that a higher dimensional space is required see https://en.wikipedia.org/wiki/Nash_embedding_theorem
ReplyDeleteUsing the Holographic Principle and recognizing that the Cosmological Horizon has the Gibbons-Hawking Temperature, Dark Energy can be viewed as the result of thermodynamic/entropic effects - and one finds that its energy density is 2/3 the Friedman Critical Total Density that makes space 'flat' (as observed!).
ReplyDeleteDavid Thornton, would the holographic principle predict that the energy density as a fraction of critical density has always been 2/3? That would be different from the cosmological constant which predicts that the ratio has increased from near zero in the early universe.
ReplyDelete"Using the Holographic Principle and recognizing that the Cosmological Horizon has the Gibbons-Hawking Temperature, Dark Energy can be viewed as the result of thermodynamic/entropic effects - and one finds that its energy density is 2/3 the Friedman Critical Total Density that makes space 'flat' (as observed!)."
ReplyDeleteReference?
Phillip H, for a 'mainstream' analysis in this regard, see the paper by Smoot et al:
ReplyDeletehttps://arxiv.org/abs/1002.4278
I have a similar shorter and slightly more heuristic analysis giving the same result. It is also supplemented by another heuristic analysis using the Principle of Maximm Force/Power advanced by Gary Gibbons and Christoph Schiller that, in addition, indicates that the total energy density must be the Friedmann Critical Density. For a relatively recent reference to the Maximum Force/Power limit in General Relativity, see the paper by Garry Gibbons and John Barrow:
https://arxiv.org/pdf/1408.1820.pdf
I had earlier sent a comment on these analyses to this blog site in connection with another discussion about the Cosmological Constant, but it didn't make it into the blog stream....
PhilG, the analysis that I mention here indeed indicates a constant 2/3 ratio, but it does include a fair bit of hand waving! On the other hand, I also have another heuristic analysis using the Kottler Metric (often called the deSitter-Schwarzschild Metric) which, using a quasi-static assumption, indicates that the Dark Energy ratio changes from 1/3 to 1 during the 'life' of the Universe and again that the total energy density always remains at the critical value (which I think is related to your perspective about total energy conservation.....)
Dear Sabine
ReplyDeleteMuch appreciated the explanation. All things being equal is what its appears to all be about.
As a non-scientist I thought I was on to something novel, some years back, when it occurred to me that a dual-universe emerging from the big-bang, one having positive energy density, the other negative energy density could explain the 120 order discrepancy of the Cosmological Constant, between its predicted and measured values. The idea being that the other universe's negative energy particles would be popping up in our universe to nicely cancel out the huge positive energy vacuum fluctuations in our universe.
ReplyDeleteBut in the last day, or two, using the term "Anti-gravitation, in Bee's search engine I came across Bee's 2006 paper titled "Anti-Gravitation" published in Physics Letter B. Turns out Andrei Linde wrote a very formal and mathematical paper on such a dual universe idea in 1988 to account for the 120 magnitude difference, plus much else. At least that's how I interpreted it, as the paper is very deep, and far beyond the level of comprehension that I'm used to in popular expositions of science.
Thank you Prof.Hossenfelder. I have recently started reading your blog and I must say there is knowledge and wisdom here not on many other physics blogs. Can you recommend a review article(s) that encompasses most of which you wrote and the discussion in the comments below?
ReplyDeleteHi Usman,
DeleteMaybe this will help. There are also many good popular science books on cosmology, eg Ethan Siegel's.
Thanks for the reference. Seeing as you are also working on modified gravitation in addition to dark matter/energy, I suppose you need to write a book on this too, especially the apparent connection between modified gravity and dark matter/energy.
Delete